S 7 行列の標準化と固有値

7.1 例題7.1 (1)

library(tidyverse)

A <- matrix(c(3,4,2,1),2,2)
eigen(A)

## eigen() decomposition
## $values
## [1]  5 -1
## 
## $vectors
##           [,1]       [,2]
## [1,] 0.7071068 -0.4472136
## [2,] 0.7071068  0.8944272

lambda <- eigen(A)$values
P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##      [,1] [,2]
## [1,]    5    0
## [2,]    0   -1

2次元平面上のベクトルとして表現．

eigenvec <- 2 * P
cardesian <- expand.grid(x = seq(-10,10,1), y = seq(-10,10,1))
trans <- cardesian
for (i in 1:nrow(cardesian)) {
  trans[i,]<-A %*% t(as.matrix(cardesian[i,]))
}
trans_eigen <- rbind(lambda,lambda) * A %*% eigenvec
bind_rows("Original" = cardesian,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,1],
        yend = eigenvec[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,2],
        yend = eigenvec[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,1],
        yend = trans_eigen[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,2],
        yend = trans_eigen[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  coord_fixed() +
  theme_classic()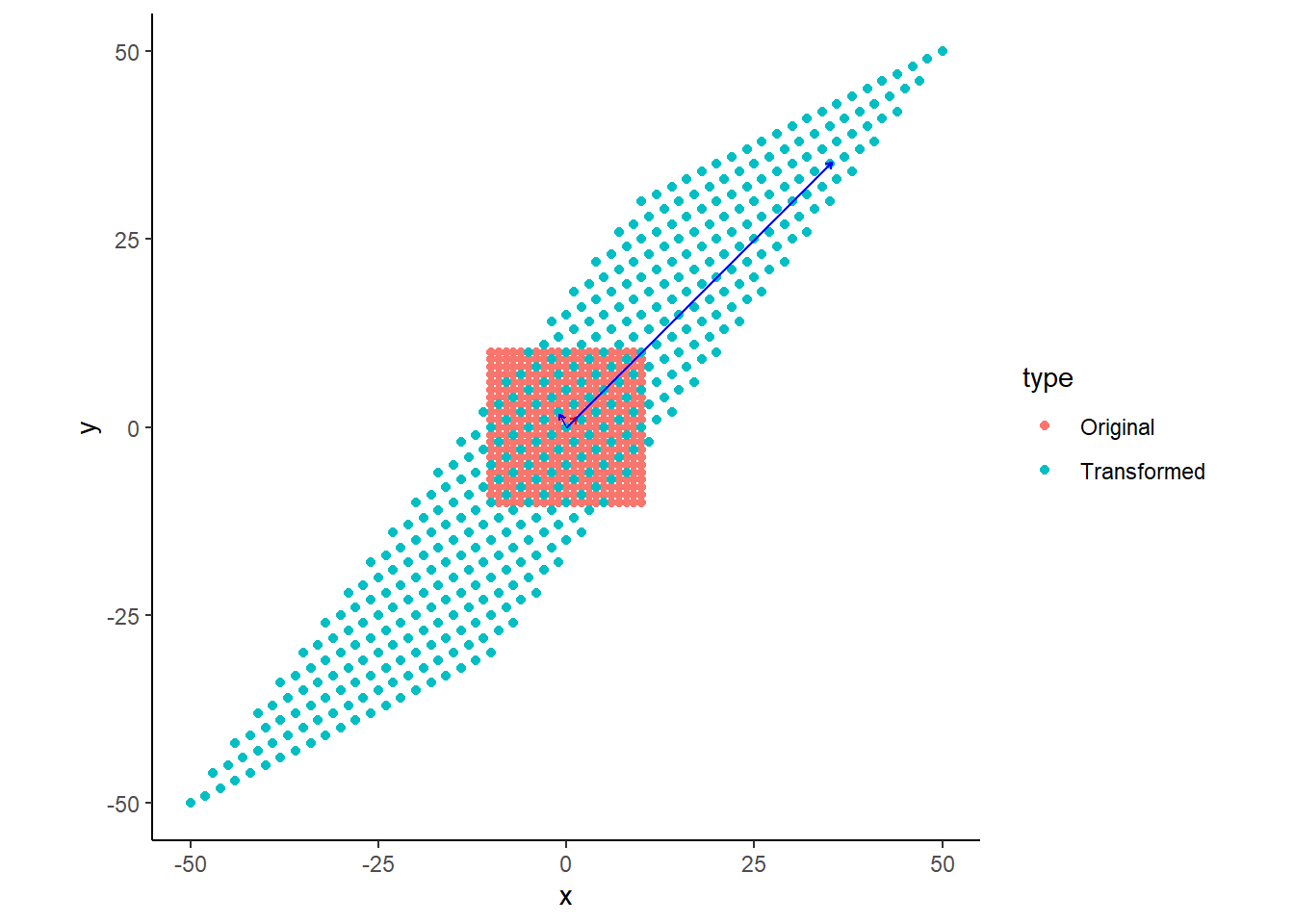

斜交軸で表現．

cardesian <- expand.grid(x = seq(-10,10,1), y = seq(-10,10,1))
cardesianP <- cardesian
for (i in 1:nrow(cardesian)) {
  cardesianP[i,]<- P %*% t(as.matrix(cardesian[i,]))
}
trans <- cardesianP
for (i in 1:nrow(cardesianP)) {
  trans[i,]<- A %*% t(as.matrix(cardesianP[i,]))
}
trans_eigen <- rbind(lambda,lambda) * A %*% eigenvec
bind_rows("Original" = cardesianP,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,1],
        yend = eigenvec[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,2],
        yend = eigenvec[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,1],
        yend = trans_eigen[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,2],
        yend = trans_eigen[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  coord_fixed() +
  theme_classic()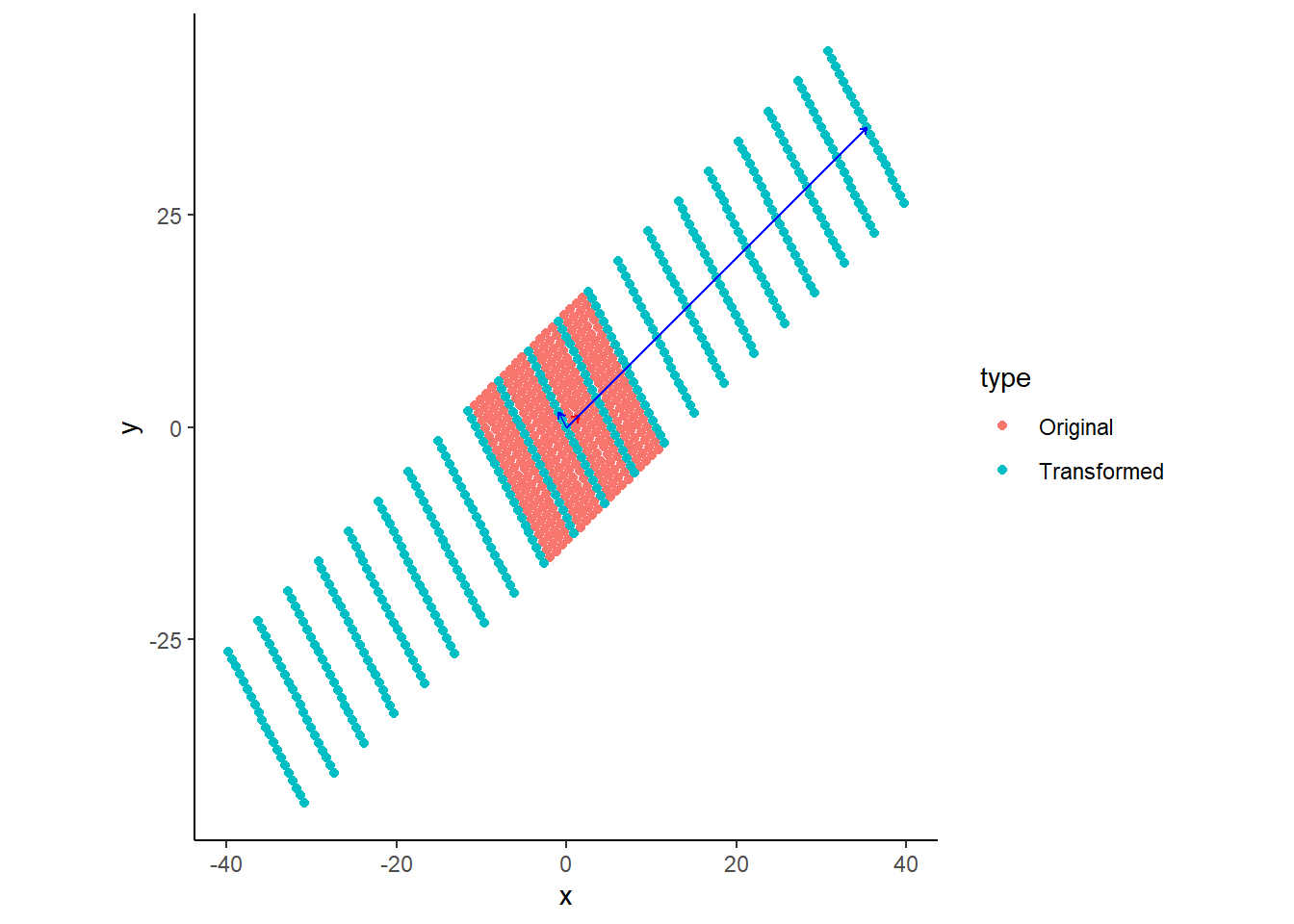

対角化でととのえる．

trans <- cardesian
for (i in 1:nrow(cardesian)) {
  trans[i,]<-A %*% P %*% t(as.matrix(cardesian[i,]))
}
bind_rows("Original" = cardesian,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  coord_fixed() +
  theme_classic()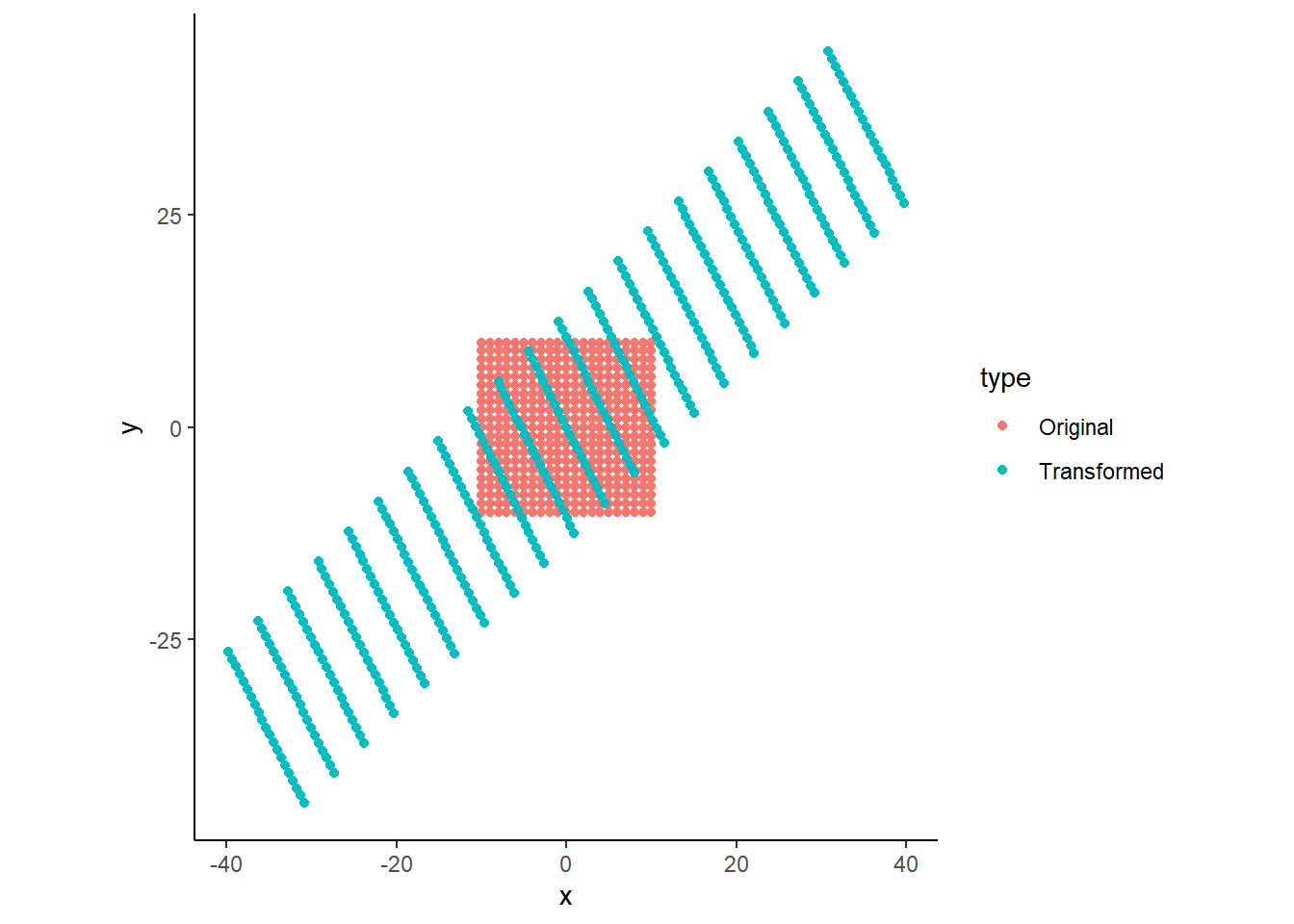

trans <- cardesian
for (i in 1:nrow(cardesian)) {
  trans[i,] <- solve(P) %*% A %*% P %*% t(as.matrix(cardesian[i,]))
}
bind_rows("Original" = cardesian,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  coord_fixed() +
  theme_classic()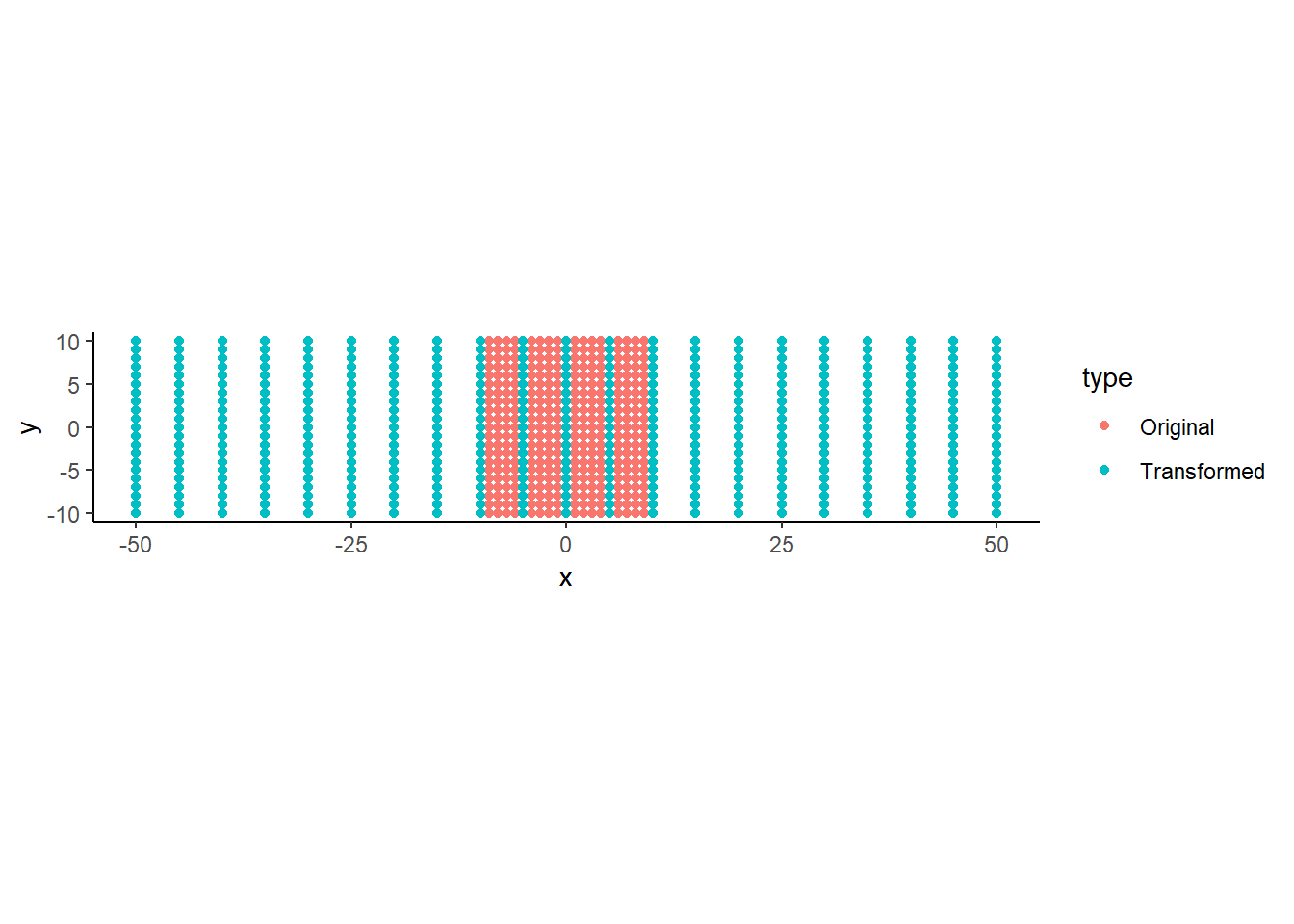

7.2 例題7.1 (2)

A <- matrix(c(5,-1,1,3),2,2)
eigen(A)

## eigen() decomposition
## $values
## [1] 4 4
## 
## $vectors
##            [,1]       [,2]
## [1,]  0.7071068 -0.7071068
## [2,] -0.7071068  0.7071068

lambda <- eigen(A)$values
P <- eigen(A)$vectors
det(P)

## [1] 4.710277e-16

\(det(P) \approx 0\)なので本来は逆行列が求められないはずだが，むりやり逆行列が求められ対角化できてしまう．正規化における誤差のせい？【要確認】 とりあえずやってみる．

round(solve(P) %*% A %*% P, digits = 10)

##      [,1] [,2]
## [1,]    4    0
## [2,]    0    4

2次元平面上のベクトルとして表現．

eigenvec <- 2 * P
cardesian <- expand.grid(x = seq(-10,10,1), y = seq(-10,10,1))
trans <- cardesian
for (i in 1:nrow(cardesian)) {
  trans[i,]<-A %*% t(as.matrix(cardesian[i,]))
}
trans_eigen <- rbind(lambda,lambda) * A %*% eigenvec
bind_rows("Original" = cardesian,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,1],
        yend = eigenvec[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,2],
        yend = eigenvec[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,1],
        yend = trans_eigen[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,2],
        yend = trans_eigen[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  coord_fixed() +
  theme_classic()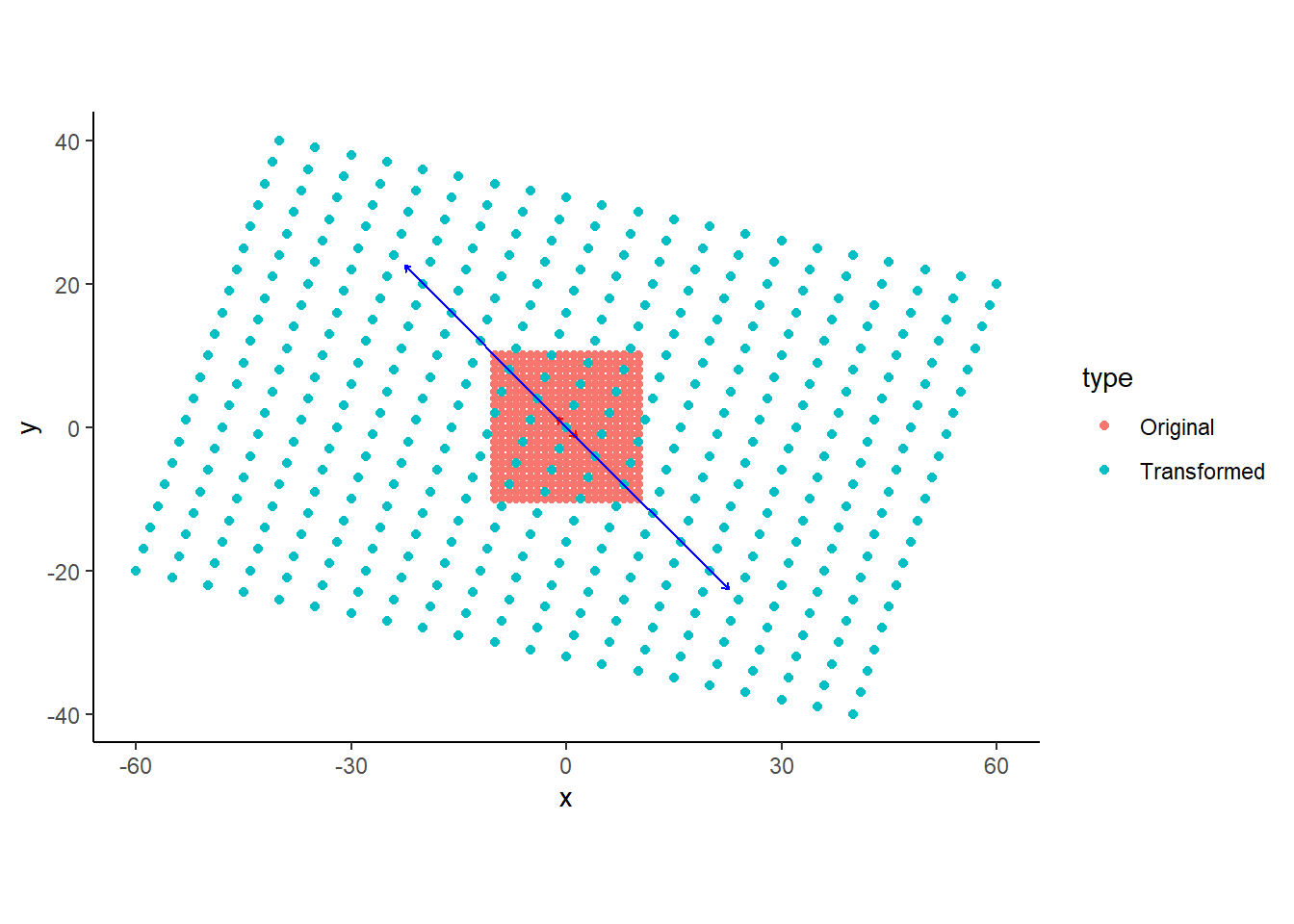

斜交軸で表現．

cardesian <- expand.grid(x = seq(-10,10,1), y = seq(-10,10,1))
cardesianP <- cardesian
for (i in 1:nrow(cardesian)) {
  cardesianP[i,]<- P %*% t(as.matrix(cardesian[i,]))
}
trans <- cardesianP
for (i in 1:nrow(cardesianP)) {
  trans[i,]<- A %*% t(as.matrix(cardesianP[i,]))
}
trans_eigen <- rbind(lambda,lambda) * A %*% eigenvec
bind_rows("Original" = cardesianP,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,1],
        yend = eigenvec[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = eigenvec[1,2],
        yend = eigenvec[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "red"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,1],
        yend = trans_eigen[2,1]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  geom_segment(
    aes(x = 0, y = 0,
        xend = trans_eigen[1,2],
        yend = trans_eigen[2,2]),
    arrow = arrow(length = unit(1, "mm")),
    color = "blue"
  ) +
  coord_fixed() +
  theme_classic()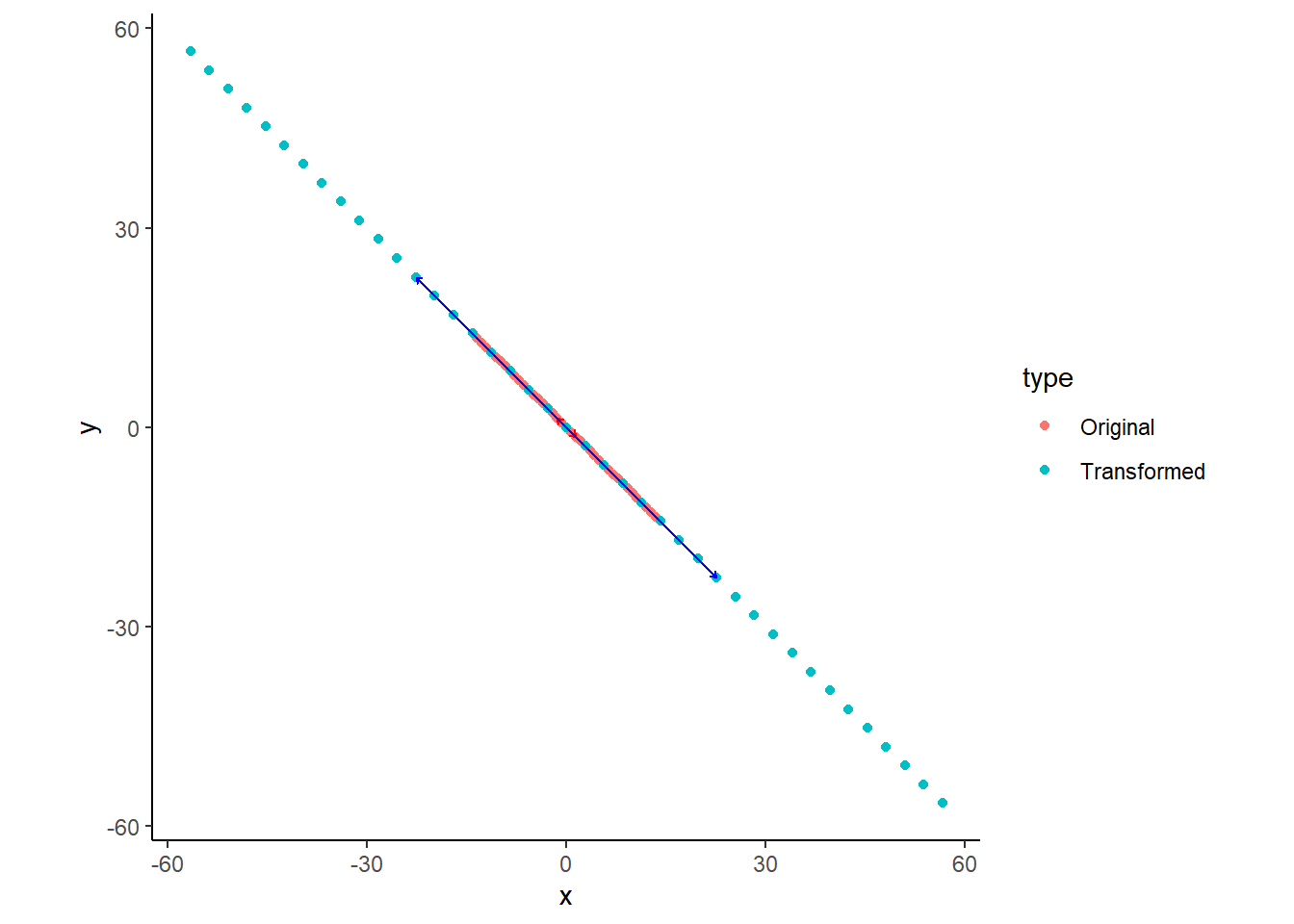

対角化でととのえる．

trans <- cardesian
for (i in 1:nrow(cardesian)) {
  trans[i,]<-A %*% P %*% t(as.matrix(cardesian[i,]))
}
bind_rows("Original" = cardesian,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  coord_fixed() +
  theme_classic()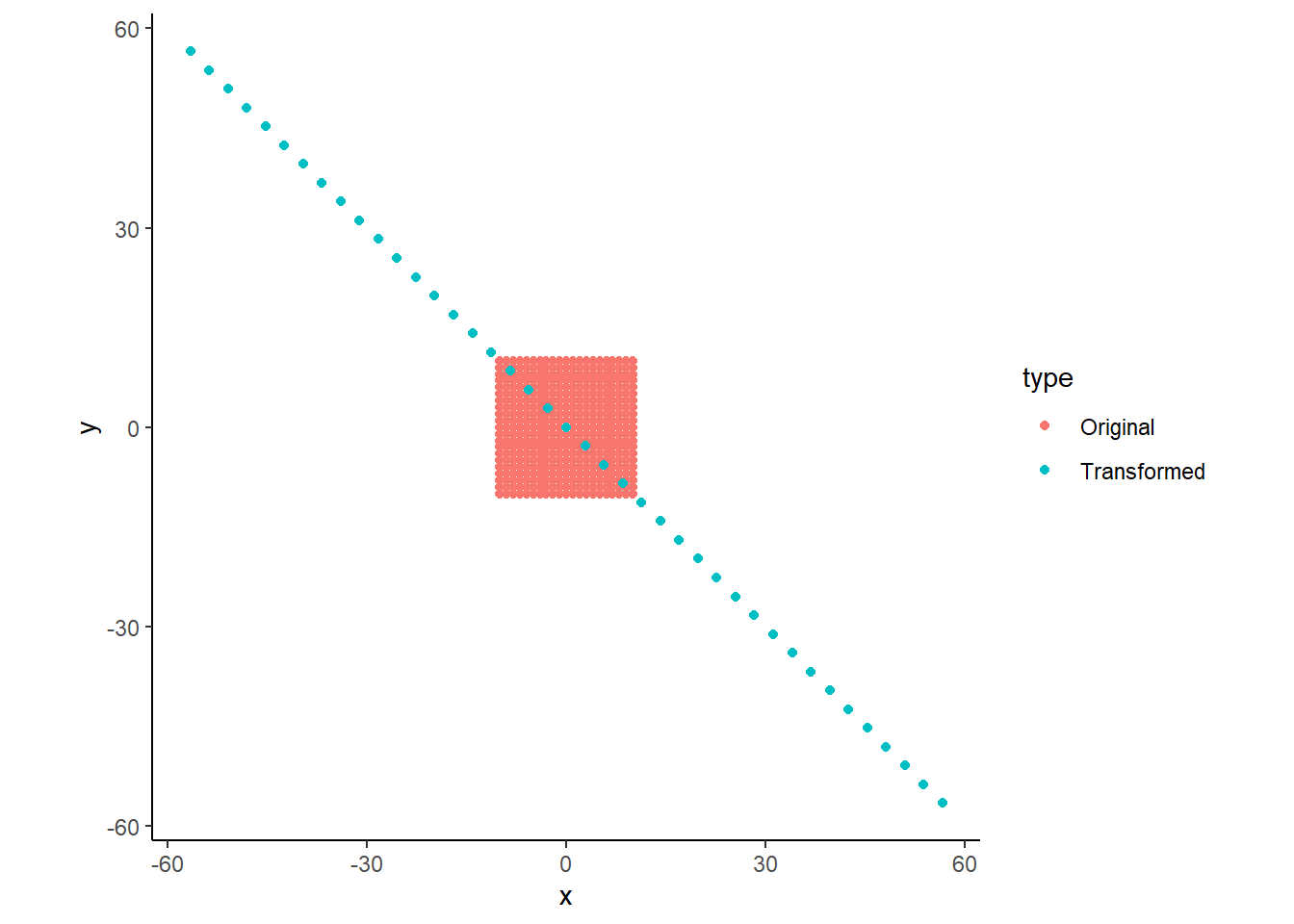

trans <- cardesian
for (i in 1:nrow(cardesian)) {
  trans[i,] <- solve(P) %*% A %*% P %*% t(as.matrix(cardesian[i,]))
}
bind_rows("Original" = cardesian,
          "Transformed" = trans,
          .id = "type") %>% 
  ggplot() + 
  geom_point(aes(x=x,y=y,color=type)) +
  coord_fixed() +
  theme_classic()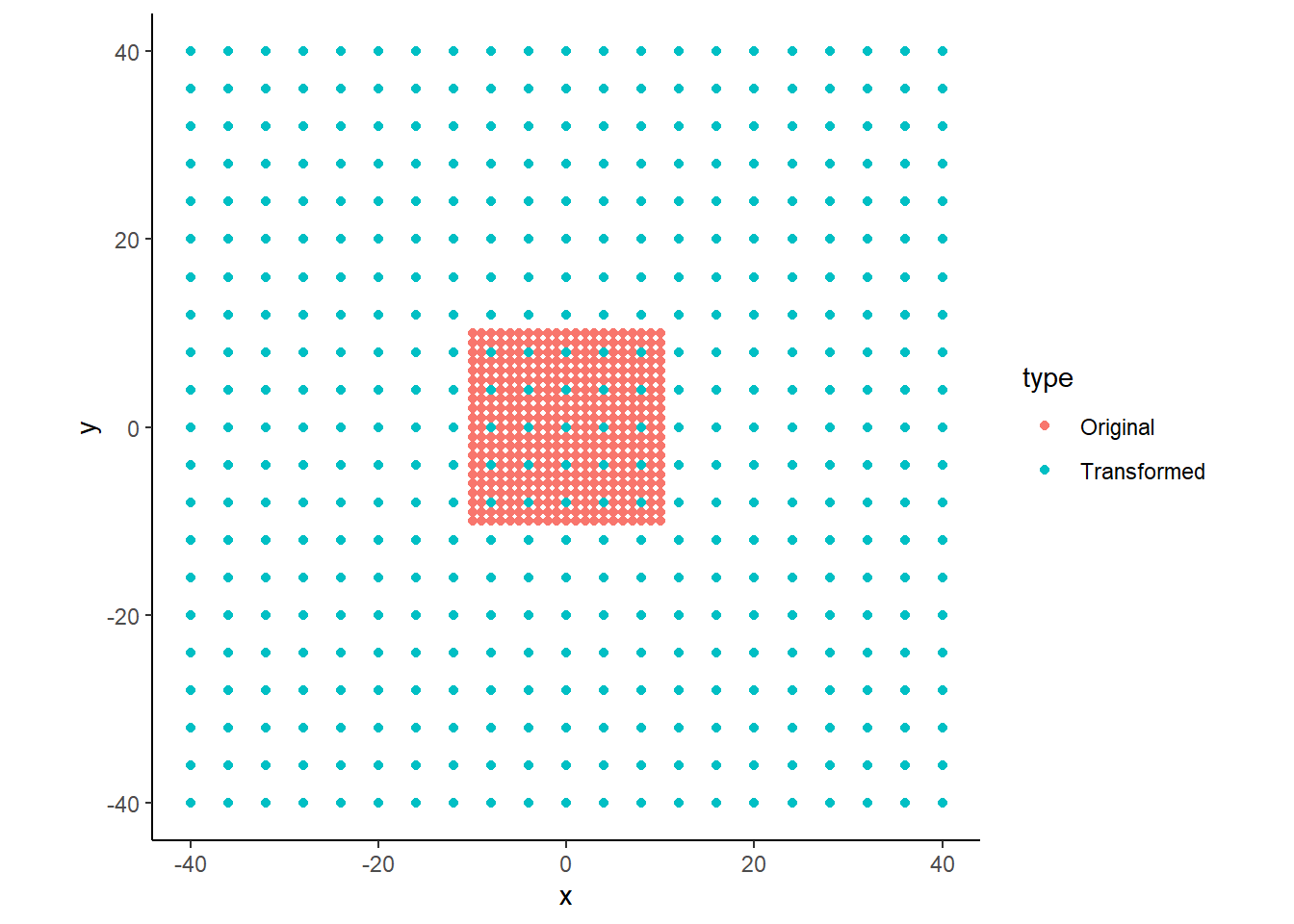

7.3 問題7.1

A <- matrix(c(3,4,2,5),2,2)
eigen(A)

## eigen() decomposition
## $values
## [1] 7 1
## 
## $vectors
##            [,1]       [,2]
## [1,] -0.4472136 -0.7071068
## [2,] -0.8944272  0.7071068

A <- matrix(c(6,2,-2,2),2,2)
eigen(A)

## eigen() decomposition
## $values
## [1] 4 4
## 
## $vectors
##           [,1]      [,2]
## [1,] 0.7071068 0.7071068
## [2,] 0.7071068 0.7071068

A <- matrix(c(2,-1,3,0),2,2)
eigen(A)

## eigen() decomposition
## $values
## [1] 1+1.414214i 1-1.414214i
## 
## $vectors
##                       [,1]                  [,2]
## [1,]  0.8660254+0.0000000i  0.8660254+0.0000000i
## [2,] -0.2886751+0.4082483i -0.2886751-0.4082483i

7.4 問題7.2

一例として．

A <- matrix(c(5,0,0,0,4,0,0,0,3),3,3)
eigen(A)

## eigen() decomposition
## $values
## [1] 5 4 3
## 
## $vectors
##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

7.5 問題7.3

A <- matrix(c(3,4,2,5),2,2)
P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##      [,1] [,2]
## [1,]    7    0
## [2,]    0    1

A <- matrix(c(6,2,-2,2),2,2)
P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##          [,1]      [,2]
## [1,] 4.00e+00 -2.98e-08
## [2,] 2.98e-08  4.00e+00

7.6 問題7.4

A <- matrix(c(1,2,0,2,2,2,0,2,3),3,3)
eigen(A)

## eigen() decomposition
## $values
## [1]  5  2 -1
## 
## $vectors
##           [,1]       [,2]       [,3]
## [1,] 0.3333333 -0.6666667 -0.6666667
## [2,] 0.6666667 -0.3333333  0.6666667
## [3,] 0.6666667  0.6666667 -0.3333333

P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##      [,1] [,2] [,3]
## [1,]    5    0    0
## [2,]    0    2    0
## [3,]    0    0   -1

7.7 演習問題7

1

A <- matrix(c(3,1,-2,2,4,-4,2,1,-1),3,3)
eigen(A)

## eigen() decomposition
## $values
## [1] 3 2 1
## 
## $vectors
##               [,1]          [,2]          [,3]
## [1,] -7.691851e-16  8.944272e-01  7.071068e-01
## [2,]  7.071068e-01 -4.472136e-01 -1.942890e-16
## [3,] -7.071068e-01  1.805948e-15 -7.071068e-01

P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##      [,1] [,2] [,3]
## [1,]    3    0    0
## [2,]    0    2    0
## [3,]    0    0    1

A <- matrix(c(2,1,1,1,2,-1,1,-1,0),3,3)
eigen(A)

## eigen() decomposition
## $values
## [1]  3  2 -1
## 
## $vectors
##              [,1]       [,2]       [,3]
## [1,] 7.071068e-01  0.5773503 -0.4082483
## [2,] 7.071068e-01 -0.5773503  0.4082483
## [3,] 1.110223e-16  0.5773503  0.8164966

P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##      [,1] [,2] [,3]
## [1,]    3    0    0
## [2,]    0    2    0
## [3,]    0    0   -1

A <- matrix(c(3,-2,1,2,-1,1,-2,2,0),3,3)
eigen(A)

## eigen() decomposition
## $values
## [1] 1.000000e+00 1.000000e+00 1.332268e-15
## 
## $vectors
##            [,1]       [,2]       [,3]
## [1,]  0.8164897  0.8017837  0.6666667
## [2,] -0.4111453 -0.5345225 -0.6666667
## [3,]  0.4053445  0.2672612  0.3333333

P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    0

A <- matrix(c(5,-11,3,2,0,3,-2,7,0),3,3)
eigen(A)

## eigen() decomposition
## $values
## [1] 3e+00+0e+00i 1e+00+6e-08i 1e+00-6e-08i
## 
## $vectors
##              [,1]          [,2]          [,3]
## [1,] 0.4082483+0i  0.5345225+0i  0.5345225-0i
## [2,] 0.4082483+0i -0.2672612+0i -0.2672612-0i
## [3,] 0.8164966+0i  0.8017837+0i  0.8017837+0i

P <- eigen(A)$vectors
round(solve(P) %*% A %*% P, digits = 10)

##                 [,1]            [,2]            [,3]
## [1,] 3e+00-0.00e+00i 0e+00-9.80e-09i 0e+00-9.80e-09i
## [2,] 0e+00+4.47e-08i 1e+00+0.00e+00i 0e+00-1.49e-08i
## [3,] 0e+00-1.49e-08i 0e+00+1.49e-08i 1e+00-0.00e+00i