第11章 ロジスティック回帰分析(1)
2回に渡ってロジスティック回帰分析の基礎を導入する.最初に回帰分析の拡張として一般化線形モデルの考え方を導入する.
11.1 一般化線形モデル
ここまで学んできた回帰分析(線形モデル)は,
- データ生成分布として正規分布を仮定し, \[Y \sim N(\mu, \sigma^2)\]
- 分布の期待値を予測する線形構造の具体的な形(変数,交互作用)を仮定 \[\eta = \beta_0 + \beta_1 x_1 + \beta_2 x_2\]
- 期待値と線形構造との関係を恒等関数として仮定, \[E[Y]=\mu = \eta\] した統計モデルであるといえる.
ここでこれらの仮定を一般化して,
- (指数分布族に属する)何らかの確率分布を仮定し, \[Y\sim \phi(\theta)\]
- 分布の期待値を予測する線形構造の具体的な形を仮定し, \[\eta = \beta_0 + \beta_1 x_1 + \beta_2 x_2\]
- 期待値と線形構造との関係を何らかの関数で仮定, \[g(\mu) = \eta\]
したモデルを考える.このようなモデルを一般化線形モデル(generalized linear model),略してGLMという.ここで,\(\eta\)を線形予測子(linear predicter),\(g(x)\)をリンク関数(link function)という.分布形,リンク関数の設定によって様々なタイプのモデルが考えられるが,通常の場合,リンク関数は分布に応じた標準的な関数を選択する(正準リンク関数).ゆえに,分布に応じてGLMの下位分類である○○回帰分析が存在する.
以下では,確率分布としてベルヌーイ分布(二項分布),正準リンク関数としてロジット関数を仮定したロジスティック回帰分析(logistic regression analysis)を導入する.
11.2 最尤推定法
GLMにおけるパラメータの推定には,確率的に最も尤もらしい推定値を選択する方法である,最尤推定法(maximum likelihood estimation)を用いる.なお,標準的な仮定のもとでの線形回帰分析においては最小二乗推定量と最尤推定量は一致する.
ここでは,ベルヌーイ分布のパラメータ推定を例として最尤推定法のさわりを導入する.
結果が2種類(たとえば,成功・失敗)しかない試行をベルヌーイ試行(Bernoulli trials)という.ベルヌーイ確率変数\(Y\)を,1もしくは0をとる変数として定める.このとき,ベルヌーイ試行における確率関数は, \[ \begin{align} P(Y=y)=f(y)=p^y(1-p)^{1-y},\qquad y=0,1 \end{align} \] と定義される.定義より \[ \begin{align*} f(y)=\left\{\begin{array}{ll} p & (y=1) \\ 1-p & (y=0) \end{array}\right. \end{align*} \] である.\(p\)はベルヌーイ試行の成功確率であり,\(1-p\)は失敗確率である.このように定義される確率分布をベルヌーイ分布(Bernoulli distribution)という.確率変数\(Y\)がベルヌーイ分布に従うことを\(Y\sim Bern(p)\)と記す.
- ベルヌーイ分布の平均 \[ \begin{align*} E[Y]=1\times p+0\times (1-p)=p \end{align*} \]
- ベルヌーイ分布の分散 \[ \begin{align*} V(Y)=(1-p)^2 p +(0-p)^2(1-p)=p(1-p) \end{align*} \]
さてここで,成功確率が\(p\)であるベルヌーイ試行を独立に\(n\)回行う.つまり\(Y_1, \cdots, Y_n\sim Bern(p)\ \mathrm{iid}\).このとき,\(Y_1, \cdots, Y_n\)の同時確率関数は \[ \begin{align} f(y_1,\cdots, y_n)=\prod_{i=1}^n p^{y_i}(1-p)^{1-y_i} \end{align} \] である.ここで,\(\prod\)はプロダクト記号と言って,総和を表す\(\sum\)のかけ算版である.成功回数の確率変数を\(Y=Y_1+ \cdots +Y_n\)とし,その実現値を\(y=y_1+\cdots +y_n\)とすると, \[\begin{align*} f(y_1,\cdots,y_n)= p^y(1-p)^{n-y} \end{align*}\] となる.いま実際に,試行を行い\(y_1, \cdots, y_n\)という結果を得た.これをデータとして二項分布のパラメータ\(p\)を推定したい.これが点推定の問題である.
最尤推定法の考え方に従って,結果\(y_1, \cdots, y_n\)を所与として,確率関数におけるパラメータ\(p\)の値を変えていったとき,結果\(y_1, \cdots, y_n\)を出力する確率\(f(y_1,\cdots,y_n)\)が最も高くなる\(p\)を「最も尤もらしい」値として採用する.
このことを調べるために,確率関数\(f\)を\(p\)を引数とする関数(尤度関数)と見なす.すなわち, \[ \begin{align} L(p) = p^{y}(1-p)^{n-y}, \end{align} \] この関数について,\(p\)の定義域における最大値を求めることが問題である.いま単純化のために\(p\in (0,1)\)とする.まず,尤度関数を対数変換すると \[ \begin{align} \log L(p) = {y}\log p + (n - y) \log(1-p) \end{align} \] となる(対数尤度関数).
このとき\(p\)について対数尤度関数を最大化する1階の必要条件は,\(p\)で微分して0と等しくなればよいので(2階の十分条件は省略), \[ \begin{align*} \frac{d \log L}{d p}=\frac{{y}}{p}-\frac{n-{y}}{1-p}=0 \end{align*} \] より, \[ \begin{align*} \frac{y}{p}=\frac{n-{y}}{1-p} \Longleftrightarrow p=\frac{{y}}{n} \end{align*} \] である.つまり,\(n\)回中成功した割合\(y/n\)が\(p\)の最尤推定値である.
11.3 最尤推定の具体例
コインを10回投げて表を1,裏が0としたとき,以下のデータを得た.\((0, 1, 1, 1, 1, 0, 1, 1, 0, 1)\),つまり\(n = 10, y =7\)である.
母数\(p\)の尤度関数・対数尤度関数は以下のようになる. \[ \begin{align*} L(p)&= p^7(1-p)^{3} \\ \log L(p)&= 7 \log p + 3\log(1-p) \end{align*} \] \(p\)の最大化問題を解くと以下を得る. \[\begin{align*} p=\frac{7}{10}=0.7 \end{align*}\]
library(tidyverse)
data <- c(0, 1, 1, 1, 1, 0, 1, 1, 0, 1)
n <- length(data)
y <- sum(data)
L_Bern <- function(p, n, y) {p^y * (1-p)^{n-y}}
tibble(
p = seq(0,1,0.01),
Lik = L_Bern(p, 10, 7),
logLik = log(Lik)
) -> lik_data
lik_data %>%
ggplot(aes(x = p, y = Lik)) +
geom_line() +
geom_vline(xintercept = 0.7, color = "red")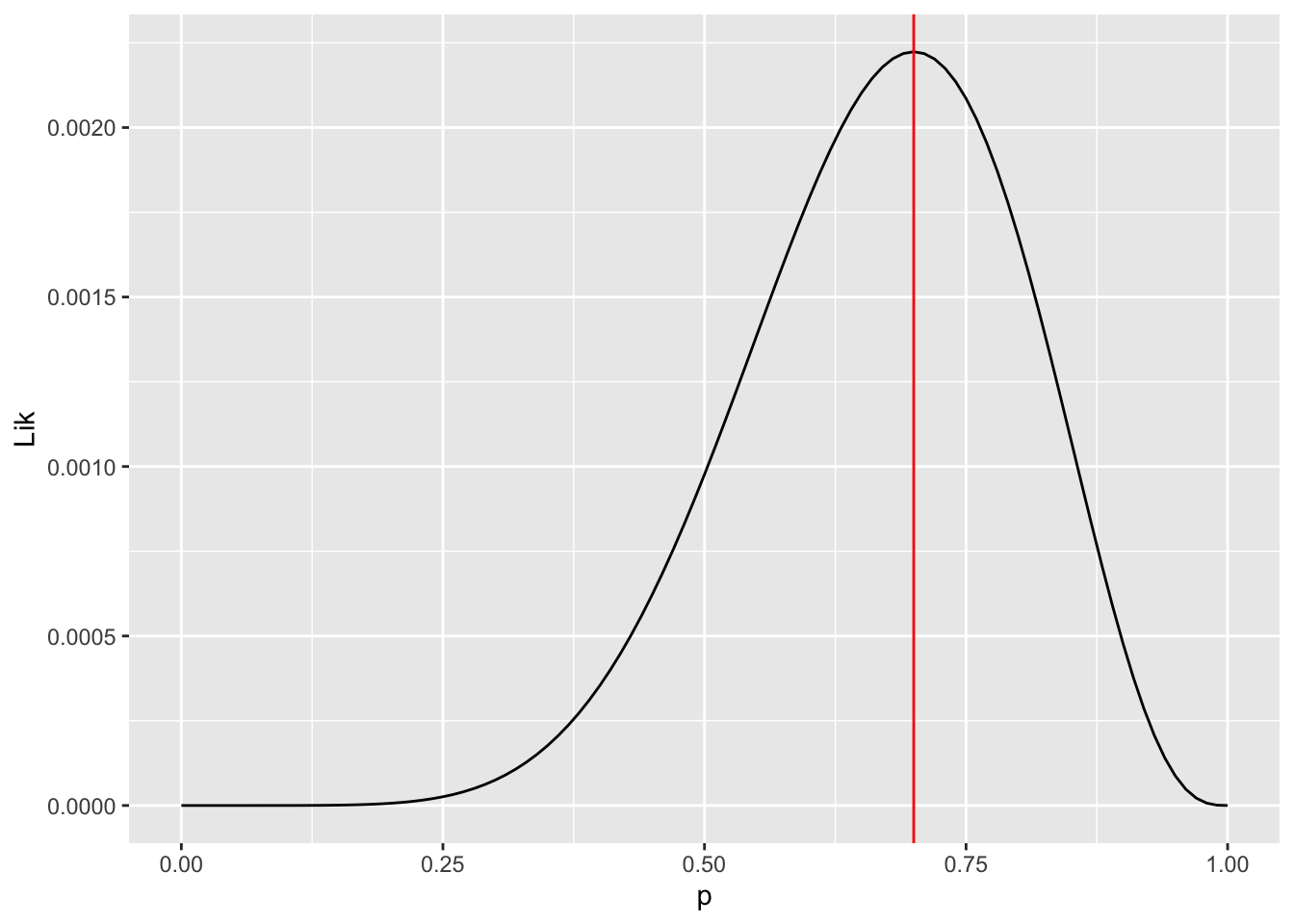
lik_data %>%
ggplot(aes(x = p, y = logLik)) +
geom_line() +
geom_vline(xintercept = 0.7, color = "red")