第2章 記述統計の復習
基本統計量や相関係数など,記述統計に関する基本的な知識を振り返る.
2.1 記述統計学とは
- 記述統計学 (descriptive statistics)とは,調査や観察,実験によって得られたデータを整理し,特性を記述するための方法論である.ここで関心の対象は「データの対象である集団そのものの特性」であり,それ以上でもそれ以下でもない.
- 一方,推測統計学 (inferential statistics)とは記述統計学の知識の上に,確率論を駆使することによって作り上げられた方法論であって,関心の対象とする集団(母集団)の一部をランダムに取り出してできる部分集団(標本)の特性を調べることで,母集団の特性を推測する技法である.
2.2 データ
- データには大きく分けて,意味のある定量的な値で与えられる量的データと,あるカテゴリーに属しているとか属していないといった情報をもつ質的データ(カテゴリカル・データ)がある.
- 量的データは,例えば,身長,体重,年齢,所得,テストの点数などである.
- 質的データは,性別,学歴,ある意見への賛否などである.
- 質的データもダミー変数化という工夫によって数量化することができる.
2.3 平均,分散,標準偏差
2.3.1 平均 (mean)
\[ \begin{align} \bar{x}=\frac{1}{n}\sum_{i=1}^n x_i=\frac{x_1+x_2+\cdots+x_n}{n} \end{align} \]
2.3.2 分散 (variance)
\[ \begin{align} \hat{\sigma}^2=\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2}{n} \end{align} \]
- Rの分散関数
var()は\(n-1\)で割る不偏分散 (unbiased variance)
2.3.3 標準偏差 (standard deviance)
\[ \begin{align} \hat{\sigma}=\sqrt{\hat{\sigma}^2}=\sqrt{\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2} \end{align} \]
- Rの標準偏差関数
sd()は不偏分散のルート
2.3.4 例(身長データ)
身長: 152.8, 150.1, 182.0, 163.2, 167.3, 160.2, 164.9, 161.4, 179.9, 172.2
\[ \begin{align*} \bar{x}=&\frac{1}{10}(152.8+150.1+182.0+163.2+167.3+160.2+164.9+161.4+179.9\\ &+172.2) \\ =&165.4 \\ \\ \hat{\sigma}^2 =&\frac{1}{10}\{(152.8-165.4)^2+(150.1-165.4)^2+(182.0-165.4)^2+(163.2-165.4)^2\\ &+(167.3-165.4)^2+(160.2-165.4)^2+(164.9-165.4)^2+(161.4-165.4)^2\\ &+(179.9-165.4)^2+(172.2-165.4)^2\}\\ =&\frac{1}{10}(158.76+234.09+275.56+4.84+3.61+27.04+0.25+16+210.25+46.24) \\ =&97.66\\ \\ \hat{\sigma}=&\sqrt{97.66}=9.88 \end{align*} \]
## [1] 165.4## [1] 97.664## [1] 9.882512.4 標準得点 (standard score)
- データ\(x_1,x_2,\cdots,x_n\)をそれぞれ\(a\)倍して,\(b\)を足すことを考える. \[ \begin{align} z_i=ax_i+b,\qquad i=1,\cdots,n \end{align} \]
- このようなデータ変換を一次変換 (linear transformation)という.このとき,変換後の平均・分散・標準偏差は以下のようになる. \[ \begin{align} \bar{z}&=\frac{1}{n}\sum_{i=1}^n\left(ax_i+b\right)=a\bar{x}+b \\ \hat{\sigma}_z^2&=\frac{1}{n}\sum_{i=1}^n (z_i-\bar{z})^2=\frac{1}{n}\sum_{i=1}^n a^2(x_i-\bar{x})^2=a^2\hat{\sigma}^2_x \\ \hat{\sigma}_z&=\sqrt{a^2\hat{\sigma}^2_x}=|a|\hat{\sigma}_x \end{align} \]
一次変換について,とくに \[ \begin{align} z_i=\frac{x_i-\bar{x}}{\hat{\sigma}_x} \end{align} \] を採用した場合,つまり, \[ \begin{align*} a=\frac{1}{\hat{\sigma}_x},\qquad b=-\frac{\bar{x}}{\hat{\sigma}_x} \end{align*} \] とすると,\(\bar{z}=0,\ \hat{\sigma}^2_z=1,\ \hat{\sigma}_z=1\)となる.このような変換を標準化(standardization)といい,\(z_i\)を(standard score)という.
ちなみに,受験の時におなじみのいわゆる「偏差値得点」は,標準得点をさらに\(10z_i+50\)と変換したものであり,平均は50,標準偏差は10となるようにしたものである.
## [1] -3.252953e-15## [1] 12.5 共分散と相関係数
2変数のデータを考える.例えば,それぞれの個人に身長と体重を尋ねたとすると,それぞれの個人について観測値ベクトル\((身長_i,体重_i)\)が求まる.これを対象者分集めたものが2変数データである.
2つの変数の結びつきを調べる上でもっとも基本となるのが,共分散(covariance)である.変数\(x\)と\(y\)の共分散を\(C_{xy}\)で表すと,以下のように定義される. \[ \begin{align} C_{xy}&=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) \\ &=\frac{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n} \nonumber \end{align} \]
2つの変数の関連が強いほど共分散はプラスもしくはマイナス方向に大きくなり,関連がなけれなないほど0に近づく.
Rの共分散
cov()はn-1で割ったもの\(x\)と\(y\)の標準得点について共分散をとったものを相関係数(correlation coefficient)という. \[ \begin{align*} z_i=\frac{x_i-\bar{x}}{\hat{\sigma}_x},\ \ \ \ w_i=\frac{y_i-\bar{y}}{\hat{\sigma}_y} \end{align*} \] とすると,相関係数\(r_{xy}\)は以下のように定義される. \[ \begin{align} r_{xy}&=\frac{1}{n}\sum_{i=1}^n z_i w_i \\ &=\frac{1}{n}\sum_{i=1}^n \left(\frac{x_i-\bar{x}}{\hat{\sigma}_x}\right)\left(\frac{y_i-\bar{y}}{\hat{\sigma}_y}\right) =\frac{C_{xy}}{\hat{\sigma}_x \hat{\sigma}_y} \end{align} \]
相関係数は\(-1\)から\(1\)の間の値をとり,\(|r_{xy}|=1\)のときそのときに限り,\(y_i=a x_i+b\)という線形の関係がすべての\(i\)について成り立っている.そして,\(|r_{xy}|\)が1に近づけば近づくほど,線形の関係に近づく.
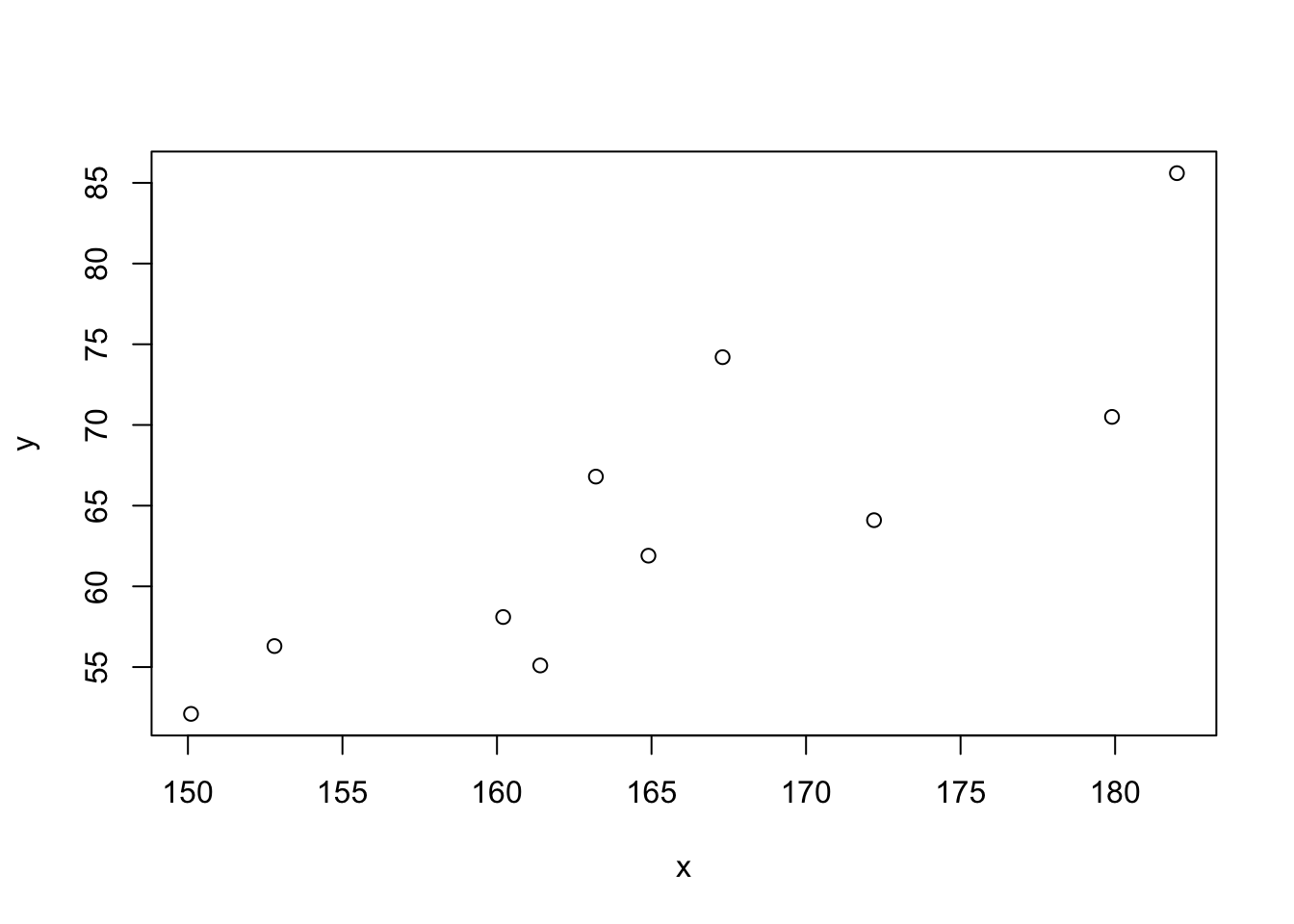
2.5.1 例(身長と体重)
身長\(x\): 152.8, 150.1, 182.0, 163.2, 167.3, 160.2, 164.9, 161.4, 179.9, 172.2
体重\(y\): 56.3, 52.1, 85.6, 66.8, 74.2, 58.1, 61.9, 55.1, 70.5, 64.1
\[ \begin{align*} C_{xy}=81.313,\ \ \ \ \hat{\sigma}_x=9.882,\ \ \ \ \hat{\sigma}_y=9.684 \\ r_{xy}=\frac{81.313}{9.882\times 9.684}=0.850 \end{align*} \]
## [1] 81.313## [1] 0.8496357## [1] 0.8496357