第3章 推測統計の復習
標本分布,母平均の推定・検定,t検定など基本的な推測統計の知識を振り返る.以下,確率論の基本的事項は既知とする.
3.1 推測統計学
われわれが調査対象としたい集団全体を母集団(population)という.母集団を全部調査することができれば(このような調査を悉皆調査という)記述統計学だけで事足りる.一方,母集団の一部を取り出し分析することで,母集団の特性を推測する場合には,確率論を基礎にする推測統計学(inferential statistics)の知識が必要不可欠である.
母集団から調査対象として選び出された対象のそれぞれを標本(sample)という.標本を選び出すことを標本抽出(sampling)という.特に,標本を等確率で選び出すことを無作為抽出(random sampling)という.
母集団の何らかの特性について,その分布を母集団分布(population distribution)という.母集団が十分に大きい場合,母集団サイズが無限の無限母集団を仮定し,母集団分布は何らかの確率分布\(f(x)\)であると仮定する.これによって,各々の標本\(X_1, X_2, \cdots, X_n\)は\(f(x)\)に従う確率変数であると見なすことができる(確率変数である標本の実現値は普通小文字で\(x_1,x_2,\cdots,x_n\)と表す).特に,無作為抽出標本の場合は「標本\(X_1, X_2, \cdots, X_n\)は,母集団分布\(f(x)\)に従う\(n\)個の独立な確率変数である」ということを仮定してよい.
3.2 標本分布
3.2.1 母平均と母分散
- ある確率分布を特定する値をパラメータあるいは母数という.特に,母集団分布の平均\(\mu\)を母平均(population mean),分散\(\sigma^2\)を母分散(population variance)という.
3.2.2 標本分布
標本\(X_1, X_2, \cdots, X_n\)を引数とする任意の関数\(f(X_1,X_2,\cdots,X_n)\)を統計量(statistic)と呼ぶ.
標本\(X_1, X_2, \cdots, X_n\)はそれぞれ母集団分布に従う確率変数であるから,統計量もまた確率的に分布する.この統計量の分布を標本分布(sampling distribution)という.
3.2.3 母分散が既知の場合の標本平均の標本分布
標本\(X_1, X_2, \cdots, X_n\)から,以下によって与えられる統計量を標本平均(sample mean)という. \[ \begin{align*} \bar{X}=\frac{1}{n}\sum_{i=1}^n X_i=\frac{X_1+ X_2+ \cdots + X_n}{n} \end{align*} \]
\(X_1,X_2,\cdots,X_n\)が独立で,すべて同一の正規分布\(N(\mu,\sigma^2)\)に従うとき,標本平均の標準化得点を \[ \begin{align*} Z_n=\frac{\sqrt{n}(\bar{X}-\mu)}{\sigma} \end{align*} \] とすると,\(Z_n\)は標準正規分布\(N(0,1)\)に従う.このことは,標本数の多少にかかわらず成立する.また,中心極限定理より,標本\(X_1,X_2,\cdots,X_n\)が独立で,平均\(\mu\)分散\(\sigma^2\)をもつ同一の分布に従っているとき,\(n\)が十分に大きいときは近似的に標準正規分布\(N(0,1)\)に従う.
3.2.4 母分散が未知の場合の標本平均の標本分布
不偏標本分散(unbiased sample variance)\(S^2\) \[ \begin{align} S^2=\frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 \end{align} \]
\(t\)統計量(\(t\) statistic) \[ \begin{align}\label{t statistic} t=\frac{\sqrt{n}(\bar{X}-\mu)}{S} \end{align} \]
\(X_1,X_2,\cdots,X_n\)が独立で,すべて同一の正規分布\(N(\mu,\sigma^2)\)に従うとき,\(t\)統計量は自由度\(n-1\)の\(t\)分布\(t(n-1)\)に従う.また,中心極限定理より,標本\(X_1,X_2,\cdots,X_n\)が独立で,平均\(\mu\)分散\(\sigma^2\)をもつ同一の分布に従っているとき,\(n\)が十分に大きいときは近似的に標準正規分布\(N(0,1)\)に従う.
標準正規分布\(N(0,1)\)から,サイズ\(n\)の標本を抽出し平均を取る操作を1000回繰り返す.その\(t\)値の分布と標準正規分布(赤)と\(t\)分布\(t(n-1)\)(青).
n <- 100
repdata <- replicate(10000, rnorm(n))
t <-apply(repdata, 2, function(x) {
(mean(x))*sqrt(n)/sd(x)
})
hist(t, prob=TRUE,xlim=c(-4,4),
breaks=seq(-ceiling(max(abs(t))),ceiling(max(abs(t))),0.2),
col="skyblue", main = paste("n =", n))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)
curve(dt(x,n-1),-4,4,col="blue",lwd=2,add=TRUE)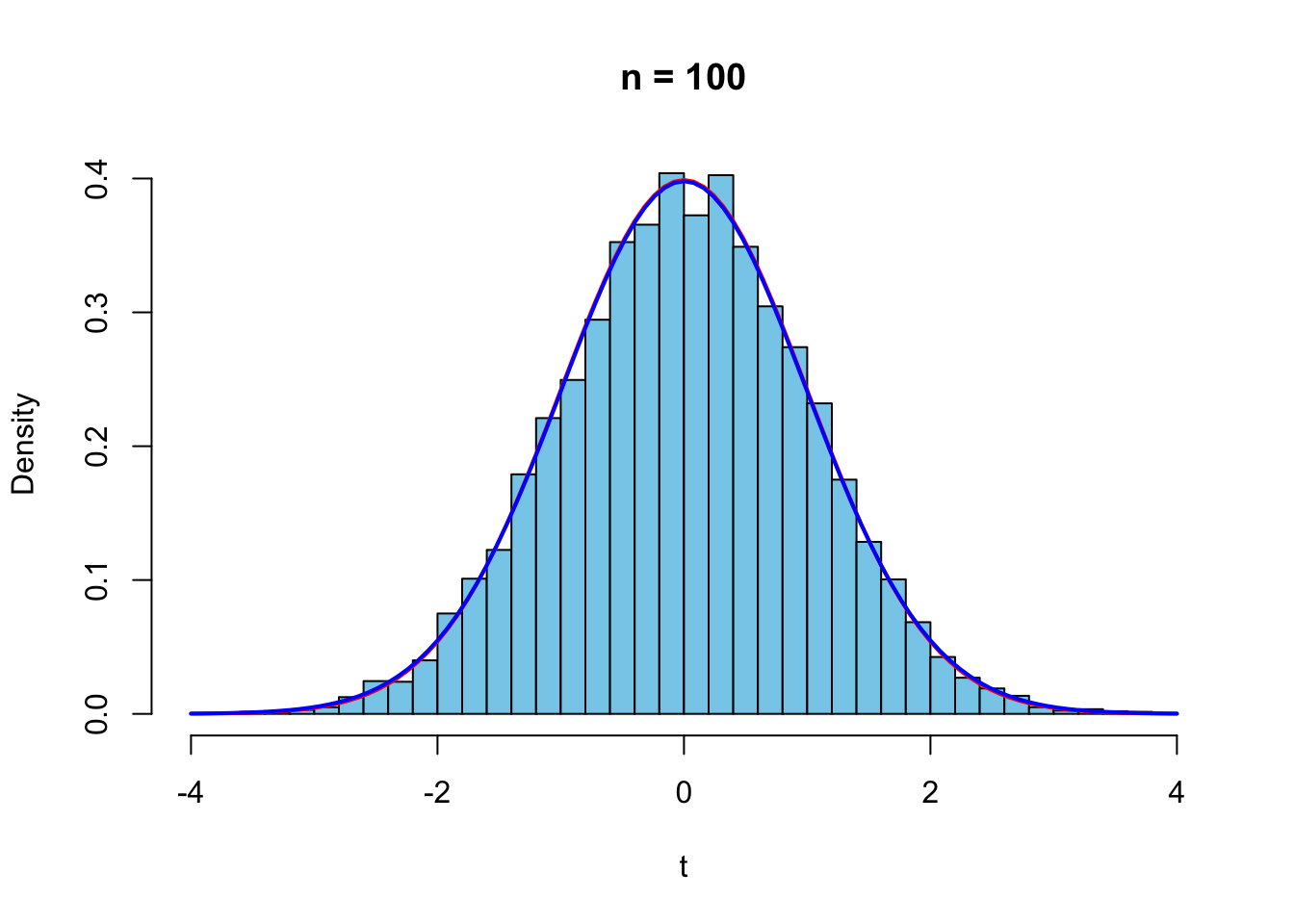
3.3 推定
3.3.1 推定量
母数を推定するために標本から求められた統計量を推定量(estimator)という.母数を一般的に\(\theta\)で表すとき,この推定量を\(\hat{\theta}\)で表す.推定量は母数の推定に用いられる統計量であるので,一般の統計量と同じく,標本\(X_1,X_2,\cdots,X_n\)の関数 \[ \begin{align*} \hat{\theta}=\hat{\theta}(X_1,X_2,\cdots,X_n) \end{align*} \] である.標本の各々は確率変数であるので,推定量\(\hat{\theta}\)もまた確率変数である.標本の各々が,ある実現値\(X_1=x_1,X_2=x_2,\cdots,X_n=x_n\)をとるとき,これを推定量に代入して得られる値のことを推定値(estimate)という.
推定には,推定値によって,母数を推定す点推定(point estimation)と,真の母数が入っている確からしい区間を求める区間推定(interval estimation)の2種類がある.
3.3.2 点推定
推定値の期待値(平均)が母数と一致するとき,この推定量を不偏推定量(unbiased estimator)という.
標本平均\(\bar{X}\)は母平均\(\mu\)の不偏推定量である.\(E(\bar{X}) = \mu\).
不偏標本分散\(S^2\)は母分散\(\sigma^2\)の不偏推定量である.\(E(S^2) = \sigma^2\).
3.4 区間推定
標本分布を活かして「母数が入っている可能性の高い区間」を推定することができる.このような方法を区間推定(interval estimation)という.
より具体的に区間推定とは,真の母数の値\(\theta\)が,ある区間\([L,U]\)に入る確率を\(1-\alpha\ \ (0\leq \alpha \leq 1)\)となるように保証する方法であり, \[\begin{align} P(L\leq \theta \leq U)= 1-\alpha \end{align}\] となる確率変数\(L,U\)の実現値を求めるものである.\(1-\alpha\)は信頼係数(confindence coefficient)と呼ばれ,このとき,区間\([L,U]\)を\(100(1-\alpha)\%\)信頼区間(confidence interval)と呼ぶ.
調査データの分析段階で\(\theta\)はすでに決まった定数であるので,\(\theta\)が確率的に動くことは想定されていない.母数\(\theta\)ではなく,区間\([L,U]\)が確率変数として標本抽出において動くと考える.
ゆえに信頼区間の経験的な解釈としては,「同じ母集団から繰り返し異なった標本をとって,その都度信頼区間を計算すると,繰り返し試行が十分に多ければ,\(\theta\)を区間内に含むものの割合が\(1-\alpha\)となる」というものである.
library(tidyverse)
CItest<-function(m,s,n,r) {
rdata<-replicate(r,{
ex<-rnorm(n,m,s)
m<-mean(ex)
ci<-1.96*sd(ex)/sqrt(n)
c(m-ci,m,m+ci)
})
rdata<-data.frame(1:r,t(rdata))
colnames(rdata)<-c("trials","minci","mean","maxci")
sr<-sum(rdata$minci<m & rdata$maxci > m)/r
cat(paste("正答率: ",sr))
ggplot2::ggplot(data = rdata, aes(x = mean ,y = trials)) +
geom_point() +
geom_errorbarh(aes(xmin=minci, xmax=maxci)) +
geom_vline(xintercept = m, color="red") +
theme_classic()
}
CItest(160,20,10,100)## 正答率: 0.9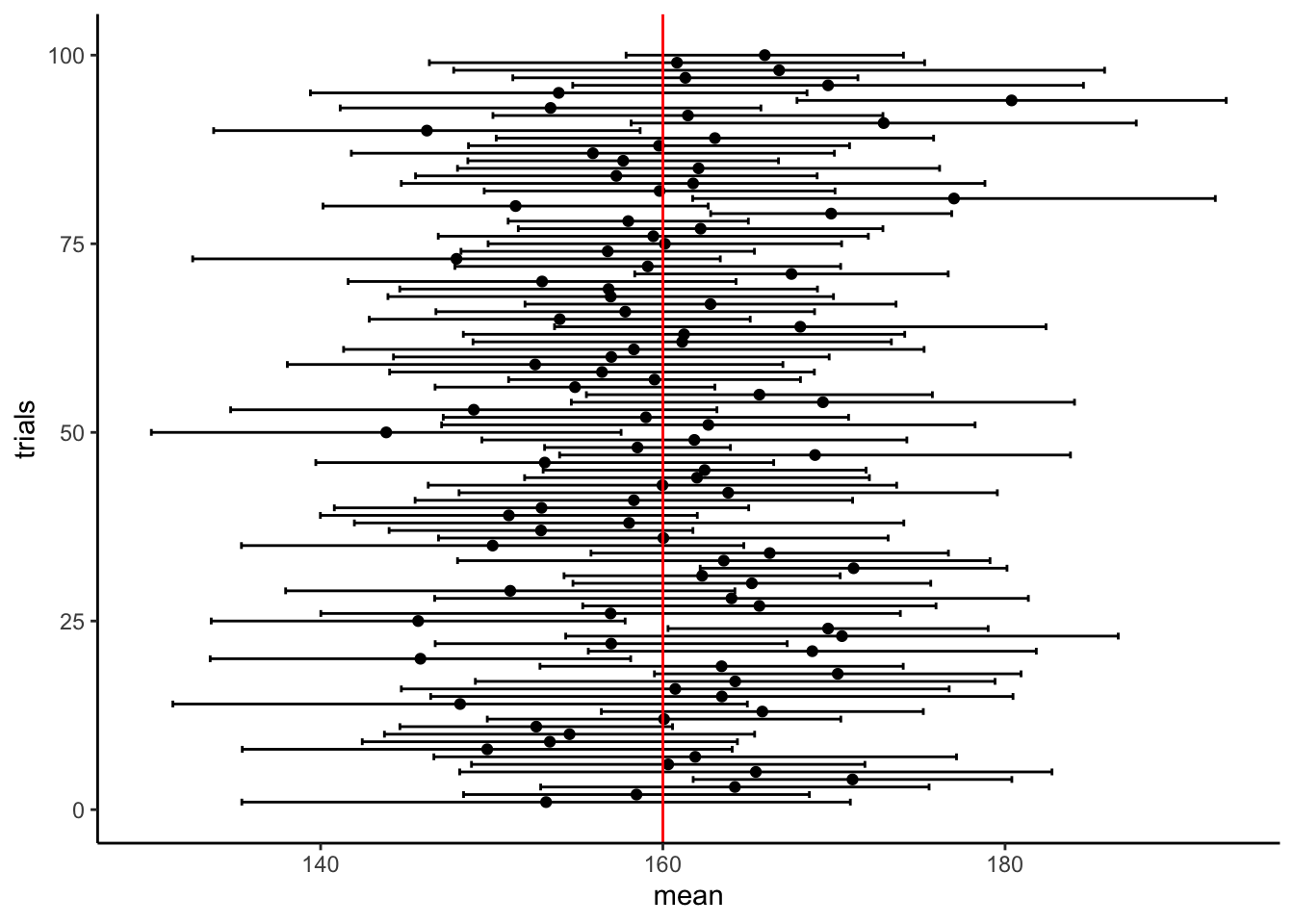
3.4.1 正規母集団,母分散が未知の場合の母平均の区間推定
\(t\)統計量は自由度\(n-1\)の\(t\)分布\(t(n-1)\)にしたがう.
自由度\(n-1\)の\(t\)分布\(t(n-1)\)において,それ以上の値が実現する確率が\(\alpha/2\)となるような値を\(t_{\alpha/2}(n-1)\)とおく.このとき,\(t(n-1)\)に従う確率変数\(t\)について \[ \begin{align}\label{CI5} P(-t_{\alpha/2}(n-1)\leq t \leq t_{\alpha/2}(n-1))=1-\alpha \end{align} \] が成り立つ.この式の左辺カッコの中に \[ \begin{align*} t=\frac{\sqrt{n}(\bar{X}-\mu)}{S} \end{align*} \] を代入してまとめると, \[ \begin{align}\label{CI6} P\left(\bar{X}-t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}}\leq \mu \leq \bar{X}+t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}}\right)=1-\alpha \end{align} \] となる.ゆえに,\(100(1-\alpha)\%\)信頼区間は \[ \begin{align} \left[\bar{X}-t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}},\ \ \bar{X}+t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}}\right] \end{align} \] によって計算できる.
例)母集団分布は正規分布であるが母分散は未知であり,標本サイズは16である.このとき,標本平均が165センチ,不偏標本分散が100センチであることが分析結果から分かった. \[ \begin{align*} t_{0.025}(15)=2.131 \end{align*} \] である.このときの,母平均の95%信頼区間は \[ \begin{align*} \left[165-2.131 \frac{10}{4},\ \ 165+2.131 \frac{10}{4}\right], \end{align*} \] まとめると,\([159.67, 170.33]\)となる.95%の確からしさで,母平均\(\mu\)は区間\([159.67, 170.33]\)に含まれると結論づけられる.
3.5 検定
仮説検定(hypothesis testing)とは,母集団について仮定された命題を,標本を調べることで検証する方法である
仮説検定のプロセス
- 母集団の特性に関して,帰無仮説(null hypothesis)\(H_0\)を設定する.同時に,帰無仮説に対立する対立仮説(alternative hypothesis)\(H_1\)を設定する.
- 有意水準(significant level)を決定する.
- 帰無仮説が正しいと仮定したときの,検定統計量(test statistics)の標本分布を導き出し,有意水準に対応する棄却域(rejection region)を求める.
- 実際の標本から統計量の実現値を計算する.
- その値が棄却域に落ちるときは,帰無仮説を棄却(reject)し対立仮説を採用(accept)する.一方,棄却域外に落ちるときは,帰無仮説は棄却されない.
3.5.1 \(p\)値
- 有意水準は理論的には,検定に先立って定めておくものであるが,多くの統計のコンピュータ・パッケージは\(p\)値(\(p\) value)を出力する.\(p\)値とは,検定統計量\(T\)の実現値が\(t_r\)だったときに,\(t_r\)が境界値になるような有意水準\(p\)の値のことである.具体的に,帰無仮説が\(\theta=\theta_0\)のとき,対立仮説を\(\theta\neq \theta_0\)とする両側検定においては, \[ \begin{align*} P(|T|>t_r| \theta=\theta_0)=p \end{align*} \] が\(p\)値となる.\(p<0.05\)であれば有意水準5%で,\(p<0.01\)であれば有意水準1%で帰無仮説は棄却できることが分かる.
3.5.2 正規母集団,母分散が未知の場合の母平均の仮説検定
帰無仮説と対立仮説を以下のように設定する \[ H_0:\ \mu = \mu_0,\quad H_1:\ \mu\neq \mu_0 \]
帰無仮説の下で\(t\)統計量 \[ \begin{align*} t=\frac{\sqrt{n}(\bar{X}-\mu_0)}{S} \end{align*} \] は自由度\(n-1\)の\(t\)分布\(t(n-1)\)に従う.\(t\)統計量を検定統計量とする.
有意水準を5%とすると\(|t|>t_{0.025}(n-1)\)が棄却域である.
標本から\(t\)値を計算して棄却域に落ちるかどうかをみる
例)母集団分布は正規分布であるが母分散は未知であり,標本サイズは16であった.このとき,標本平均が165センチ,不偏標本分散が100センチであることが分析結果から分かった.\(t\)統計量は \[ \begin{align*} t=\frac{4(165-160)}{10}=2 \end{align*} \] である.5%水準の両側検定の場合,棄却域は \[ \begin{align*} |t|>t_{0.025}(15)=2.131 \end{align*} \] であるので,5%水準では帰無仮説は棄却されない.
Rを用いた区間推定と検定の例(\(H_0: \mu = 160\))
##
## One Sample t-test
##
## data: x
## t = 0.18714, df = 9, p-value = 0.8557
## alternative hypothesis: true mean is not equal to 160
## 95 percent confidence interval:
## 153.6858 167.4532
## sample estimates:
## mean of x
## 160.5695