第10章 重回帰分析(3)
ダミー変数を入れたモデル,交互作用モデルについて理解する.
10.1 具体例
以下のよう散布図データを考える.単純に単回帰分析を行うと以下のようになる.
library(tidyverse)
set.seed(8931)
tibble(
x = runif(100, 0, 50),
y = rnorm(100, 2 * x + 10, 10),
d = rep(0, 100)
) %>%
bind_rows(
tibble(
x = runif(100, 0, 50),
y = rnorm(100, x + 50, 10),
d = rep(1, 100)
)
) -> data
data %>%
ggplot(aes(x=x, y=y)) +
geom_point() +
geom_smooth(method="lm", fill=NA, lwd=1.5, fullrange=TRUE) +
theme_classic()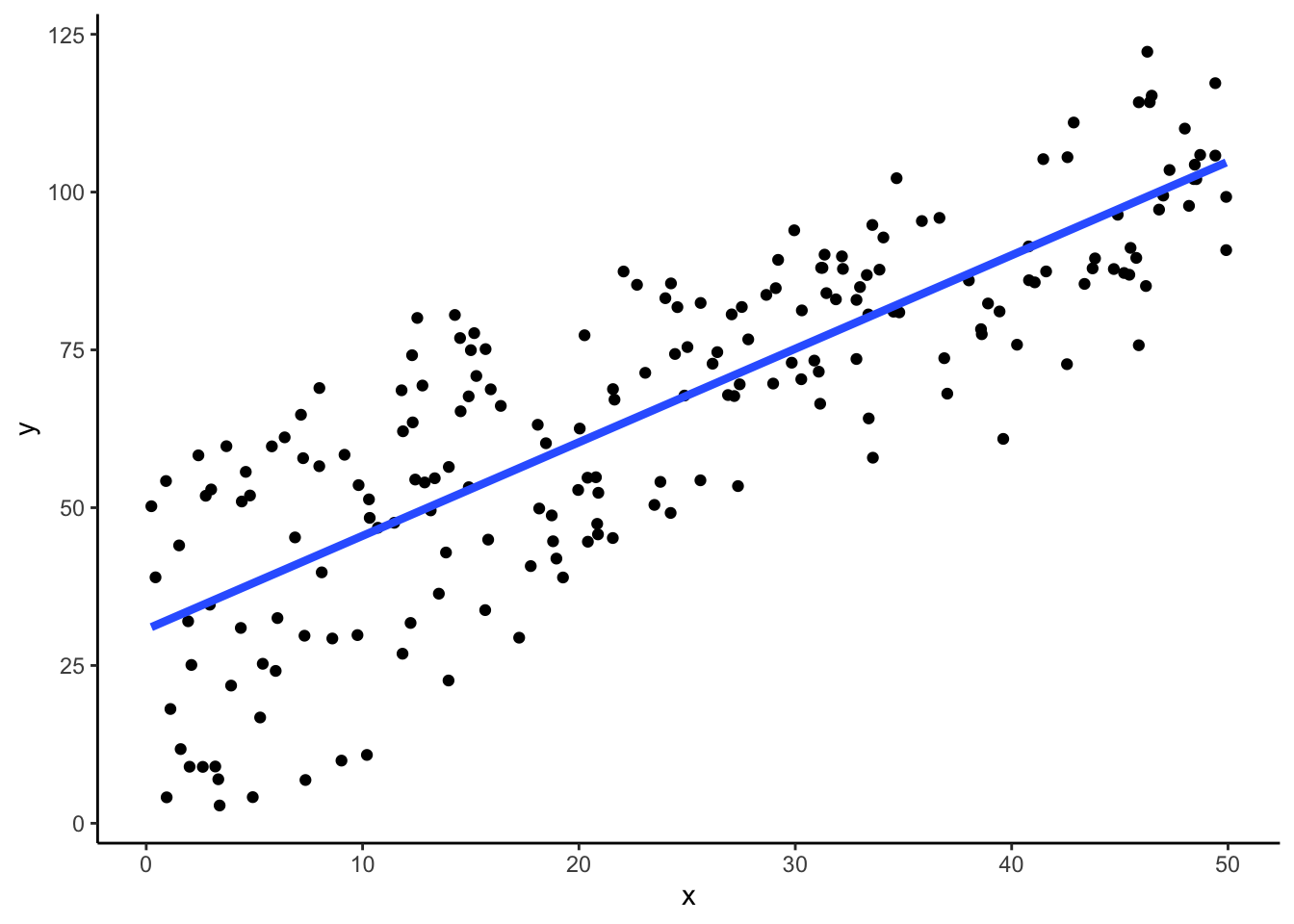
\[ Y = \beta_0 + \beta_1 x + \varepsilon,\quad \varepsilon \sim N(0, \sigma^2) \]
##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -35.010 -10.481 0.201 12.005 30.769
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 30.72624 2.01699 15.23 <2e-16 ***
## x 1.48176 0.07281 20.35 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15 on 198 degrees of freedom
## Multiple R-squared: 0.6766, Adjusted R-squared: 0.6749
## F-statistic: 414.2 on 1 and 198 DF, p-value: < 2.2e-16まあ,これでもよさそうではある.
10.2 ダミー変数を投入したモデル
しかし,データの構造を精査すると,背後に何らかの特性のカテゴリー(グループ)の違いがあって,カテゴリーの違いが一部\(Y\)の違いを生み出しているかもしれない.たとえば,年収を年齢に回帰させるモデルを考える場合,そもそも性別で年収の平均値が異なっていると考えるのは,経験的には理に適っている.
そこで,母集団がある特性について2つの排反なカテゴリーにわかれるとき,その所属を識別する変数としてダミー変数(dummy variable)\(d\)を導入する.それらのカテゴリーの一方(たとえば性別でいう女性)にあてはまるとき\(d=1\),もう一方(たとえば男性)にあてはまるときは\(d=0\)とする.これによって2つのカテゴリーの違いをモデルに組み込むことができる.
ちなみに,一般的に\(n\geq 2\)以上のカテゴリーに分かれる場合,\(n-1\)個のダミー変数を用意すれば十分である.たとえば,「松竹梅」という3区分があるとき,\(d_松, d_竹\)という2つのダミー変数を用意する.このとき, \[ \begin{align} 松:\ & d_松 = 1, d_竹 = 0 \\ 竹:\ & d_松 = 0, d_竹 = 1 \\ 梅:\ & d_松 = 0, d_竹 = 0 \\ \end{align} \] と表すことができる.この場合の「梅」は基準カテゴリー(reference category)と言われる.
Rの場合,factor変数をlmに投入すれば自動的に必要なダミー変数を作ってくれる.このとき,レベルの一番最初のカテゴリーが基準カテゴリーとなる.
以下,ダミー変数が1つの場合を説明する.ダミー変数を投入したモデルは以下のようになる. \[ Y = \beta_0 + \beta_1 x + \beta_2 d + \varepsilon,\quad \varepsilon \sim N(0, \sigma^2) \] ここで,\(d=0,1\)を代入すると以下のようになる(誤差項は省略). \[ \begin{align} d = 0 :\ & Y = \beta_0 + \beta_1 x \\ d = 1 :\ & Y = (\beta_0 + \beta_2) + \beta_1 x \\ \end{align} \] つまり,\(\beta_0\)は\(d = 0\)のカテゴリー(たとえば男性)に対応した切片,\(\beta_2\)は\(d = 1\)のカテゴリー(たとえば女性)に対応した切片の増分を示す.つまり,\(\beta_2\)は\(d = 0\)の基準カテゴリーと比べて,\(d = 1\)の時の切片がどれくらい大きいか(小さいか)を示している.このモデルでは傾きはカテゴリー共通で切片のみが変わることに注意せよ.
##
## Call:
## lm(formula = y ~ x + d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -33.180 -7.518 1.158 9.062 30.683
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.44724 1.89047 10.82 <2e-16 ***
## x 1.53667 0.05865 26.20 <2e-16 ***
## d 17.97073 1.70872 10.52 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 12.03 on 197 degrees of freedom
## Multiple R-squared: 0.7929, Adjusted R-squared: 0.7908
## F-statistic: 377 on 2 and 197 DF, p-value: < 2.2e-16\[ \hat{Y} = 20.45 + 1.54 * x + 17.97 * d \] ここから,\(d=0\)の時の切片は20.45,\(d=1\)の時の切片は\(20.45 + 17.97 = 38.42\)と推測されていることがわかる.
data %>%
ggplot(aes(x=x, y=y, color=factor(d))) +
geom_point() +
geom_function(fun = function(x) b_d[1] + b_d[2] * x,
color = "#F8766D", lwd=1.5) +
geom_function(fun = function(x) b_d[1] + b_d[3] + b_d[2] * x,
color = "#00BFC4", lwd=1.5) +
theme_classic()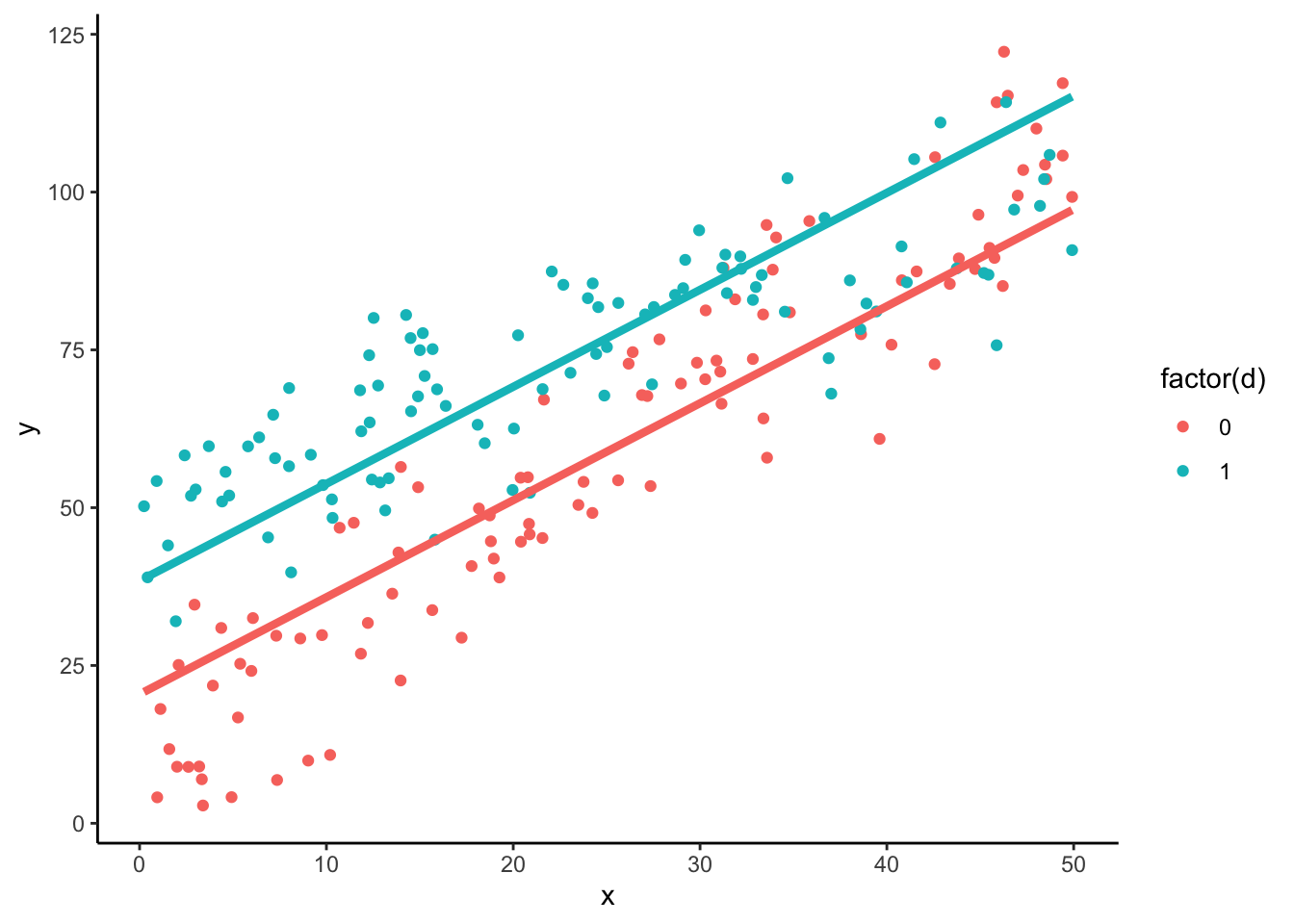
10.3 交互作用モデル
ダミー変数を投入したモデルは,切片だけが動くモデルであったが,カテゴリーに応じて傾き\(x\)と\(y\)の関連性も変わるケースがある.性別と年齢・年収で言えば,年収の基礎的な値が変わるだけではなく,年齢に応じた年収の上がり方も性別で異なるような場合である.こうした違いを表現するために交互作用項(intersection term)を投入したモデルを考える.
\[ Y = \beta_0 + \beta_1 x + \beta_2 d + \beta_3 x d+ \varepsilon,\quad \varepsilon \sim N(0, \sigma^2) \] ここで,\(d=0,1\)を代入すると以下のようになる(誤差項は省略). \[ \begin{align} d = 0 :\ & Y = \beta_0 + \beta_1 x \\ d = 1 :\ & Y = (\beta_0 + \beta_2) + (\beta_1 + \beta_3) x \\ \end{align} \] \(\beta_2\)による切片の増分の表現に加えて,以下が示される.\(\beta_1\)は\(d = 0\)のカテゴリー(たとえば男性)に対応した傾き,\(\beta_3\)は\(d = 1\)のカテゴリー(たとえば女性)に対応した傾きの増分を示す.つまり,\(\beta_3\)は\(d = 0\)の基準カテゴリーと比べて,\(d = 1\)の時の傾きがどれくらい大きいか(小さいか)を示している.このモデルでは切片・傾きともにカテゴリーに応じて変わることに注意せよ(ちなみに,切片共通で傾きのみ変わるモデルも考えられるが,ここでは取り上げない).
Rのlmでは,交互作用モデルはy ~ x * dもしくはy ~ x + d + x:dと表現する.
##
## Call:
## lm(formula = y ~ x * d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -26.6956 -7.2368 0.1071 6.4178 21.5698
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.86720 1.92800 5.118 7.35e-07 ***
## x 1.96227 0.06632 29.589 < 2e-16 ***
## d 39.66186 2.69685 14.707 < 2e-16 ***
## x:d -0.92463 0.09775 -9.459 < 2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.997 on 196 degrees of freedom
## Multiple R-squared: 0.8578, Adjusted R-squared: 0.8556
## F-statistic: 394.1 on 3 and 196 DF, p-value: < 2.2e-16\[ \hat{Y} = 9.87 + 1.96 * x + 39.66 * d - 0.92 * x * d \]
\[ \begin{align} d = 0 :\ & Y = 9.87 + 1.96 * x \\ d = 1 :\ & Y = 49.53 + 1.04 * x \\ \end{align} \]
もとの理論的構造をほぼ推定できている.また自由度調整済み決定係数も上昇している.
data %>%
ggplot(aes(x=x, y=y, color=factor(d))) +
geom_point() +
geom_function(fun = function(x) b_i[1] + b_i[2] * x,
color = "#F8766D", lwd=1.5) +
geom_function(fun = function(x) b_i[1] + b_i[3] + (b_i[2] + b_i[4]) * x,
color = "#00BFC4", lwd=1.5) +
theme_classic()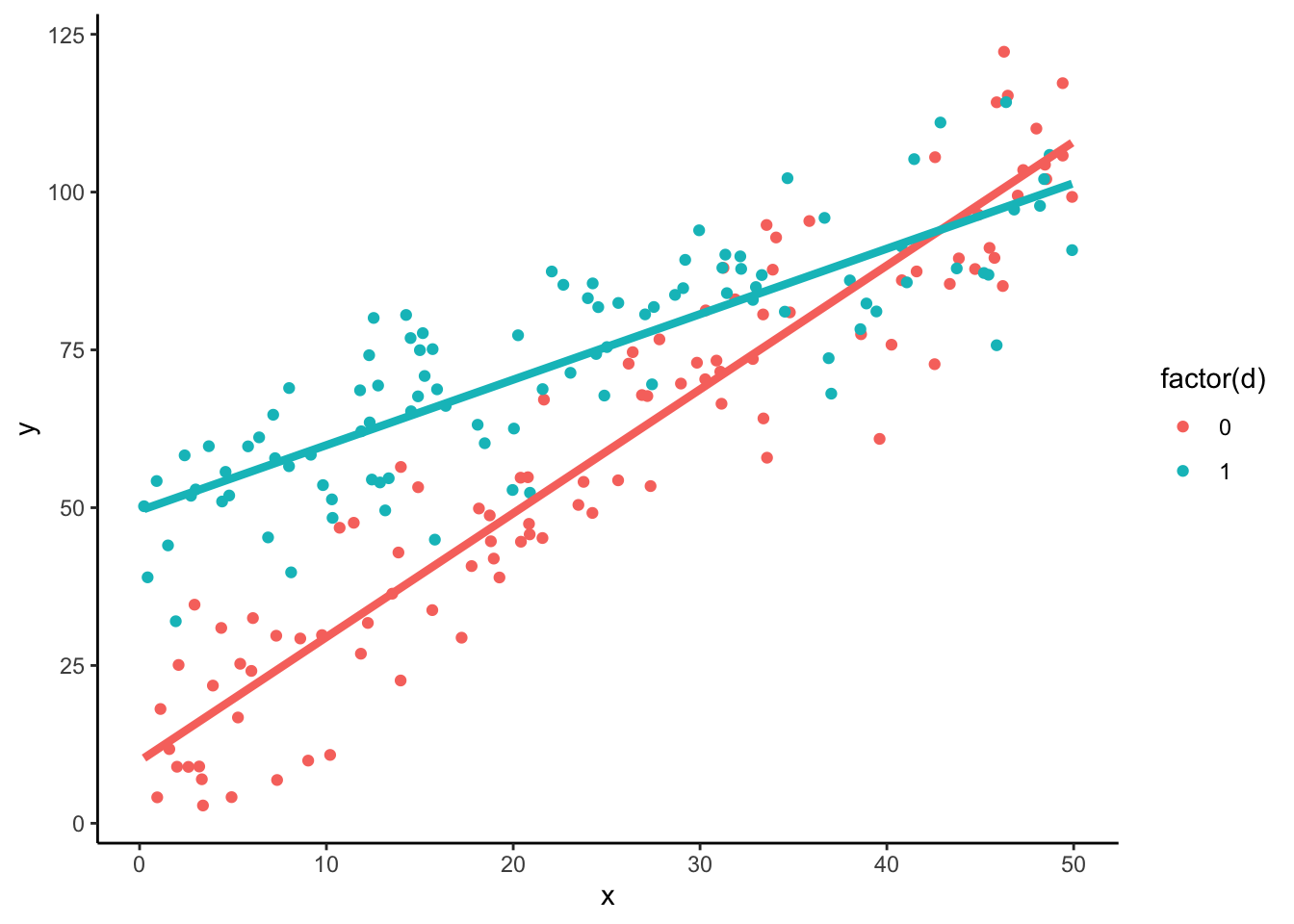
上のグラフは以下のようにggplotのgeom_smoothでも直接書ける.