第6章単回帰分析(1)

今回は確率を入れない記述的な単回帰分析について理解する．

6.1 記述的な単回帰分析

記述的な意味での回帰分析(regressoin analysis)，とくに独立変数（説明変数）が1つの単回帰分析は，散布図上に散布図のちらばりを要約する直線を引くことに他ならない．たとえば，以下の散布図上の青色の直線が回帰直線である．

library(tidyverse)

set.seed(8931)
data <- tibble(
  x=runif(100, 0, 50),
  y=rnorm(100, x + 10, 10)
)

data %>%
  ggplot(aes(x=x, y=y)) +
  geom_point() +
  geom_smooth(method="lm", fill=NA, lwd=1.5, fullrange=TRUE)+
  theme_classic()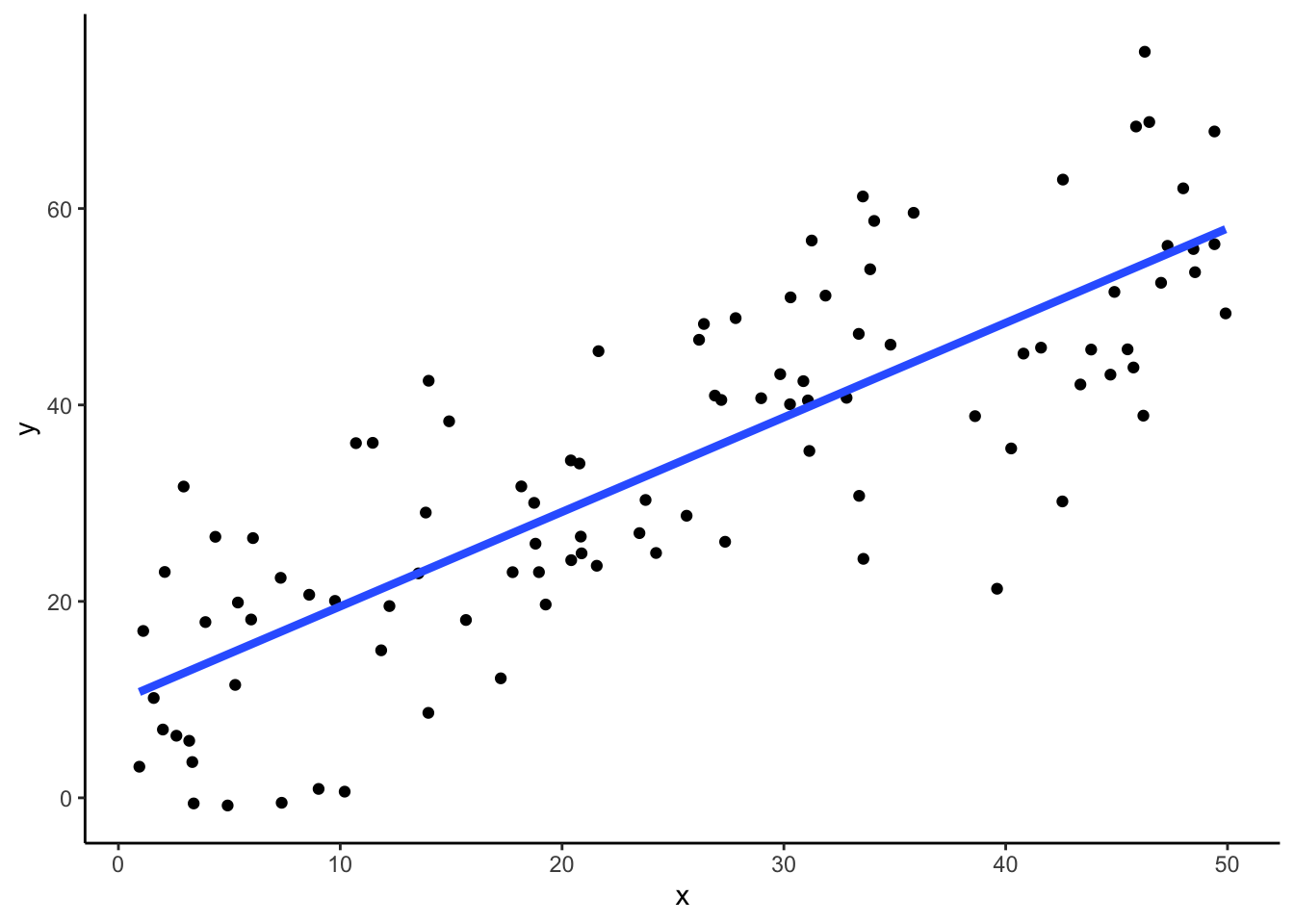

\(x\)を独立変数（制約なく動く変数），\(y\)を従属変数（\(x\)の変化に伴って変化する変数）とすると，直線 \[ \begin{align} y=b_0+b_1 x \end{align} \] の係数\(b_0, b_1\)として，散布図を表現する最適のものを選ぶ問題となる．\(b_0\)は\(x=0\)のときの\(y\)の値を示し切片(intercept)という．\(b_1\)は\(x\)一単位当たりの増加に対応する\(y\)の増分を示し傾き(slope)という．また回帰分析の文脈では，\(b_1\)をとくに，回帰係数(regression coefficient)という．またこのようなモデルを立てることを，「\(y\)を\(x\)に回帰させる」という場合がある．

ここで以下の説明の便宜のため，直線の式を次のように書き換えておく． \[ \begin{align} y=b_0+b_1 x = a_0 + b_1 (x - \bar{x}),\quad a_0 = b_0 + b_1 \bar{x} \end{align} \] こうすると，問題は散布図を表現する最適の\(a_0, b_1\)を選択する問題となる．

6.2 最小二乗法

これを解くために，散布図上の点\((x_i,y_i)\)のそれぞれについて \[ \begin{align} y_i= a_0 + b_1 (x_i - \bar{x}) + e_i \end{align} \] という関係を仮定する．ここで，\(e_i\)は点\((x_i,y_i)\)の直線\(y = a_0 + b_1 (x - \bar{x})\)からの\(y\)方向の残差である．この残差平方和 \[ \begin{align} S_e=\sum_{i=1}^n e_i^2 =\sum_{i=1}^n(y_i - a_0 - b_1 (x_i - \bar{x}))^2 \end{align} \] を最小にする\(a_0,b_1\)の値を求めることを最小二乗法(least square method)という．

\(a_0,b_1\)の最小化問題を解くためには，\(a_0,b_1\)それぞれで\(S_e\)を偏微分してゼロとおく（二階の条件はここでは無視する）． \[ \begin{align} \frac{\partial S_e}{\partial a_0}&=-2\sum_{i=1}^n(y_i - a_0 - b_1 (x_i - \bar{x}))=0\\ \frac{\partial S_e}{\partial b_1}&=-2\sum_{i=1}^n(y_i - a_0 - b_1 (x_i - \bar{x}))(x_i - \bar{x})=0 \end{align} \] これをまとめることで正規方程式と呼ばれる連立方程式を得る． \[ \begin{align} a_0 n + b_1 \cdot 0 &= \sum y_i\\ a_0 \cdot 0 + b_1 S_{xx} &= S_{xy} \label{normal_equation2} \end{align} \] ここで，以下を用いた． \[ \begin{align} & \sum_{i=1}^n (x_i - \bar{x}) = 0 \\ S_{xx} &= \sum_{i=1}^n (x_i - \bar{x})^2\\ S_{xy} &= \sum_{i=1}^n (x_i - \bar{x})y_i = \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \end{align} \] 正規方程式からただちに以下を得る． \[ a_0 = \bar{y},\quad b_0 = \bar{y} - b_1 \bar{x}, \quad b_1 = \frac{S_{xy}}{S_{xx}} = \frac{C_{xy}}{\hat{\sigma}_x^2} \] 係数\(b_0, b_1\)は，データ\(x_i, y_i\)の平均，分散，共分散から得られることが分かった．

6.3 行列による表現

\[ \begin{align*} \mathbf{y}=\left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \\ \end{array} \right],\ \mathbf{X}=\left[ \begin{array}{cc} 1 & x_1-\bar{x}\\ 1 & x_2-\bar{x}\\ \vdots & \vdots \\ 1 & x_n-\bar{x}\\ \end{array} \right],\ \mathbf{b}=\left[ \begin{array}{c} a_0 \\ b_1 \\ \end{array} \right],\ \mathbf{e}=\left[ \begin{array}{c} e_1 \\ e_2 \\ \vdots \\ e_n \\ \end{array} \right] \end{align*} \] ただし，\(a_0=b_0+b_1\bar{x}\)である．回帰式は \[\mathbf{y} = \mathbf{X}\mathbf{b} + \mathbf{e}\] 残差平方和は \[S_e=\mathbf{e}'\mathbf{e}\] である（以下，ダッシュ記号\('\)は転置を表す）．\(\mathbf{X}\)同士の積（グラム行列）とその逆行列，また\(\mathbf{X}'\mathbf{y}\)が以下のようになることに注意する． \[ \begin{align} \mathbf{X}'\mathbf{X}=\left[ \begin{array}{cc} n & 0 \\ 0 & S_{xx} \\ \end{array} \right],\ \ (\mathbf{X}'\mathbf{X})^{-1}=\left[ \begin{array}{cc} 1/n & 0 \\ 0 & 1/S_{xx} \\ \end{array} \right],\ \ \mathbf{X}'\mathbf{y}=\left[ \begin{array}{cc} \sum_{i=1}^n y_i \\ S_{xy} \\ \end{array} \right] \end{align} \] ここから正規方程式と，\(\mathbf{b}\)の解が求まる．ただし，\(\mathbf{X}'\mathbf{X}\)が正則である（逆行列が存在する）ことが解の存在条件である． \[\mathbf{X}'\mathbf{X}\mathbf{b}=\mathbf{X}'\mathbf{y} \Longleftrightarrow \mathbf{b}=(\mathbf{X}'\mathbf{X})^{-1}\mathbf{X}'\mathbf{y}\]

6.4 分散の分解

残差平方和\(S_e\)に求められた\(b_0, b_1\)を代入してまとめる．\(S_{yy}=\sum (y_i-\bar{y})^2, S_R=S_{xy}^2/S_{xx}\)とおくと以下のようになる． \[ \begin{align} S_{yy} &= S_R + S_e\\ \sum (y_i-\bar{y})^2 &= \sum (b_0+b_1 x_i-\bar{y})^2 + \sum (y_i - (b_0+b_1 x_i))^2 \end{align} \]

つまり，\(y\)の分散成分は平均から回帰直線までのばらつきである\(S_R\)と回帰直線から\(y\)までのばらつきである\(S_e\)に分解できる．\(y\)のばらつきを回帰直線だけで表現できる程度が大きいほど，回帰直線としてはうれしい．そこで， \[ R^2 = \frac{S_R}{S_{yy}} = 1 - \frac{S_e}{S_{yy}} \] を決定係数(coefficient of determination)として定義する．決定係数は「\(y\)の変動のうち，回帰によって説明できる変動の割合」を示し，1に近いほどデータに近似するという意味で回帰式の性能がよい．定義より，\(R^2 = (r_{xy})^2\)である．

6.5 分析例

Rで回帰分析をする場合はlm()関数を利用する．

lm(y ~ x, data) -> lm_res
coef(lm_res) # lm_res$coefficients

## (Intercept)           x 
##   9.8672048   0.9622678

summary(lm_res)$r.squared

## [1] 0.6616069

分散共分散情報で係数を求める．

mx <- mean(data$x)
sxx <- var(data$x) * (length(data$x) - 1)
my <- mean(data$y)
syy <- var(data$y) * (length(data$y) - 1)
sxy <- cov(data$x, data$y) * (length(data$x) - 1)
# b1
b1 <- sxy / sxx
b1

## [1] 0.9622678

# b0
my - b1 * mx

## [1] 9.867205

# R^2
(sxy)^2 / (sxx * syy)

## [1] 0.6616069

行列でもとめる．

X <- matrix(c(rep(1, nrow(data)), data$x - mx), ncol = 2)
y <- data$y
b <- solve(t(X) %*% X) %*% t(X) %*% y
# a0, b1
b

##            [,1]
## [1,] 33.7882271
## [2,]  0.9622678

# b0
b[1] - b[2] * mx

## [1] 9.867205

6.6 本日の課題

Rスクリプトを実行した結果をWordにコンパイルしたファイルをLUNA提出

第6章 単回帰分析(1)