第12章 ロジスティック回帰分析(2)

一般化線形モデルの1つとしてのロジスティック回帰分析を導入する．

12.1 一般化線形モデルの1つとしてのロジスティック回帰分析

一般化線形モデルでは，以下の3点を仮定する．

  1. （指数分布族に属する）何らかの確率分布 \[Y\sim \phi(\theta)\]
  2. 分布の期待値を予測する線形構造の具体的な形（線形予測子） \[\eta =\mathbf{X}\mathbf{\beta}\]
  3. 期待値と線形構造との関係（リンク関数） \[g(\mu) = \eta\]

一般化線形モデルの1つであるロジスティック回帰分析(logistic regression analysis)では，標準的に以下を仮定する．

  1. ベルヌーイ分布（二項分布） \[Y\sim Bern(p)\]
  2. 線形予測子 \[\eta =\mathbf{X}\mathbf{\beta}\]
  3. ロジットリンク \[\mathrm{logit}(p) = \eta\]

12.2 ロジット関数・ロジスティック関数

以下の関数をロジット関数(logit function)とよぶ． \[ \mathrm{logit}(p)=\log \left(\frac{p}{1-p}\right)\quad (0<p<1) \] \(p\)を何らかの事象が起こる確率（成功確率）とすると，\(p/(1-p)\)をオッズ(odds)という．オッズは成功確率と失敗確率の比である．つまり，失敗に比べて何倍成功しやすいかを示す．オッズの対数を取ったものを対数オッズ(log odds)という．ロジット関数は確率を引数として対数オッズを出力するものであるといえる．

library(tidyverse)

tibble(
    p = seq(0.01,0.99,0.01),
    odds = p / (1 - p),
    log_odds = log(odds)
) -> logit_data

logit_data %>%
    ggplot(aes(x = p, y = log_odds)) +
    geom_line()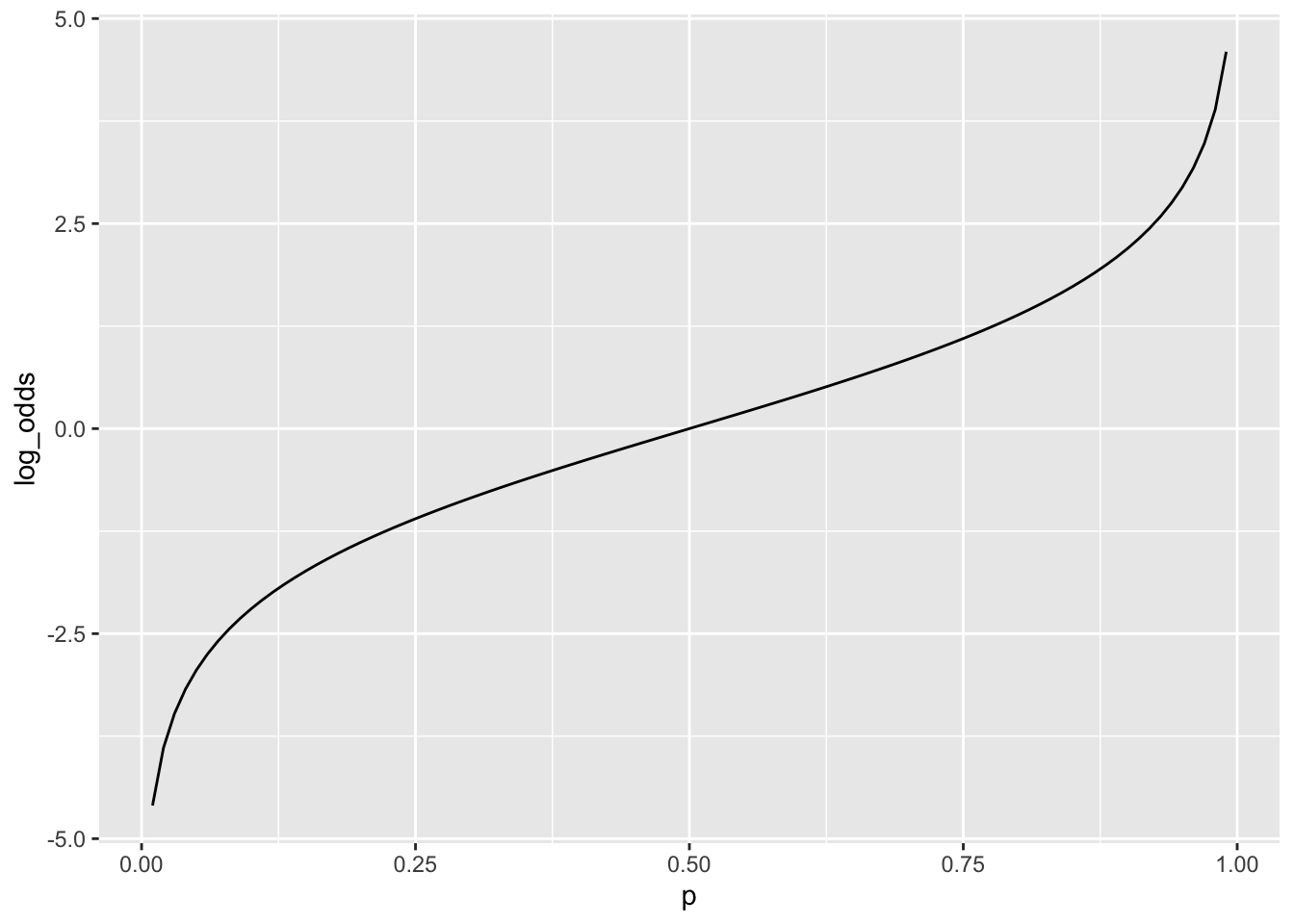

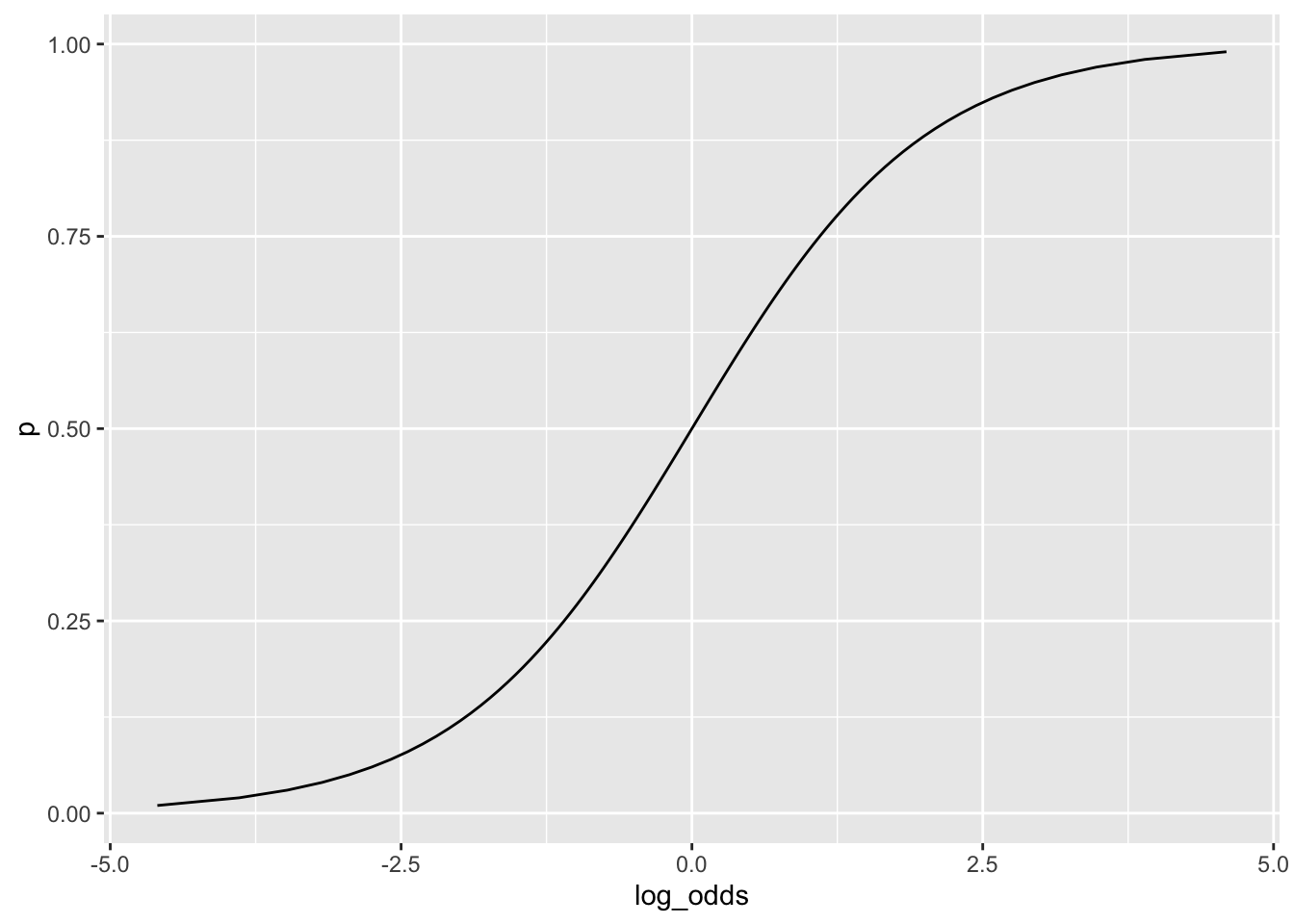
\[ \log\left(\frac{p}{1-p}\right) = \eta \] としたとき，両辺の指数を取ってまとめると以下を得る． \[ p = \frac{\exp(\eta)}{1+\exp(\eta)}=\frac{1}{1+\exp(-\eta)} \] この関数\(p = \mathrm{logistic}(\eta)\)は，ロジット関数の逆関数でありロジスティック関数(logistic function)と呼ばれる．

logit_data %>%
    ggplot(aes(x = log_odds, y = p)) +
    geom_line()

12.3 ロジスティック回帰分析

以下のモデルをロジスティック回帰分析(logistic regression analysis)という．

\[ Y_i \sim Bern(p_i),\quad \mathrm{logit}(p_i) = \mathbf{x}_i \beta = \beta_0 + \beta_1 x_{i1} + \cdots \]

データ\((x_{i1}, \cdots, y_i)\)からパラメータ\(\beta\)を最尤推定する．

推定された回帰係数\(\hat{\beta}_1\)の意味について見ていこう．ここでは独立変数は1つとする．まず， \[ \frac{d}{d x_1}\mathrm{logit}(p_i) = \hat{\beta}_1 \]

なので，回帰係数は対数オッズの\(x_1\)の増加に関する増分（減少分）を示す．つまり，\(x_1\)一単位の増加で対数オッズがどれだけ増加（減少）するかを示す．0は増加減少なし，プラスは増加，マイナスは減少，数字の大きさがどれくらい増加（減少）するかを示す．Rのglm()では回帰係数，標準誤差，仮説検定に関連するz値，p値が報告される．基本的には，lm()と同様の結果の見方でよい．

一方，回帰式の両辺の指数を取れば以下のようになる． \[ \frac{p}{1-p} = \exp(\hat{\beta}_0)\exp(\hat{\beta}_1x_1) \]

ここで，\(x'_1 = x_1 + 1\)つまり，\(x_1\)を1単位増加させると， \[ \frac{p'}{1-p'} = \exp(\hat{\beta}_0)\exp(\hat{\beta}_1x'_1) = \exp(\hat{\beta}_0)\exp(\hat{\beta}_1x_1)\exp(\hat{\beta}_1) \] ここから，以下の関係を得る． \[ \frac{p'}{1-p'}\left/\frac{p}{1-p} \right.= \exp(\hat{\beta}_1) \] つまり，回帰係数の指数（\(\exp(\hat{\beta}_1)\)）は，\(x_1\)の1単位増加に対するオッズの倍率（オッズ比(odds ratio)）を示す．1は増加減少なし，1以上は増加，1以下は減少を示す．解釈のしやすさからこちらも併せて報告されることがある．

12.4 AIC

最尤推定法では，モデルの当てはまりの指数として最尤法で用いた対数尤度関数の値（最大対数尤度，\(\log L\)）を用いる．もっとも一般的な指数はAIC(赤池情報量規準)とよばれ，以下で定義される． \[\mathrm {AIC} =-2\log L+2k\] ここで\(k\)は独立変数の数で，AICの値が低いほど相対的なモデルの予測性能の良さを示す．独立変数を加えていく場合，AICの値が下がるかどうかを見る．

12.5 具体例

\(x_1, x_2\)の変化に従って，\(Y\)の発生の仕方が異なるかをロジスティック回帰分析で検討する．たとえば，年収\(x_1\)と地域\(x_2\)（ダミー変数）にしたがって結婚\(Y\)のしやすさが変わるかどうかである．

set.seed(8931)
data <- tibble(
    x1 = sort(runif(100, 0, 100)),
    x2 = sample(c(0, 1), 100, replace=TRUE),
    p = (1 + exp(-(-10 + 0.2*x1 + 2 * x2)))^(-1),
    y = sapply(p, function(x) rbinom(1, 1, x))
)

glm(y ~ x1, data = data, 
    family = binomial(link = "logit")) -> m1 # family = binomialだけでもよい
summary(m1)
## 
## Call:
## glm(formula = y ~ x1, family = binomial(link = "logit"), data = data)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -7.98257    1.95427  -4.085 4.41e-05 ***
## x1           0.18033    0.04315   4.179 2.93e-05 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 137.628  on 99  degrees of freedom
## Residual deviance:  35.788  on 98  degrees of freedom
## AIC: 39.788
## 
## Number of Fisher Scoring iterations: 7

まずx1のみのモデルであるが，回帰係数は0.18033，指数化係数はexp(0.18033) = 1.197613，1%水準で有意である．つまり，x1一単位の増加で対数オッズが0.18上昇する．あるいはオッズ比は1.2倍である．つまり，x1はyの実現に効果がある．

以下の図はx1とyの散布図と，ロジスティック回帰で推定された\(\hat{p}\)である．

data %>%
  mutate(
    p_hat = m1$fitted.values
  ) %>%
  ggplot() +
  geom_point(aes(x = x1, y = y)) +
  geom_line(aes(x = x1, y = p_hat))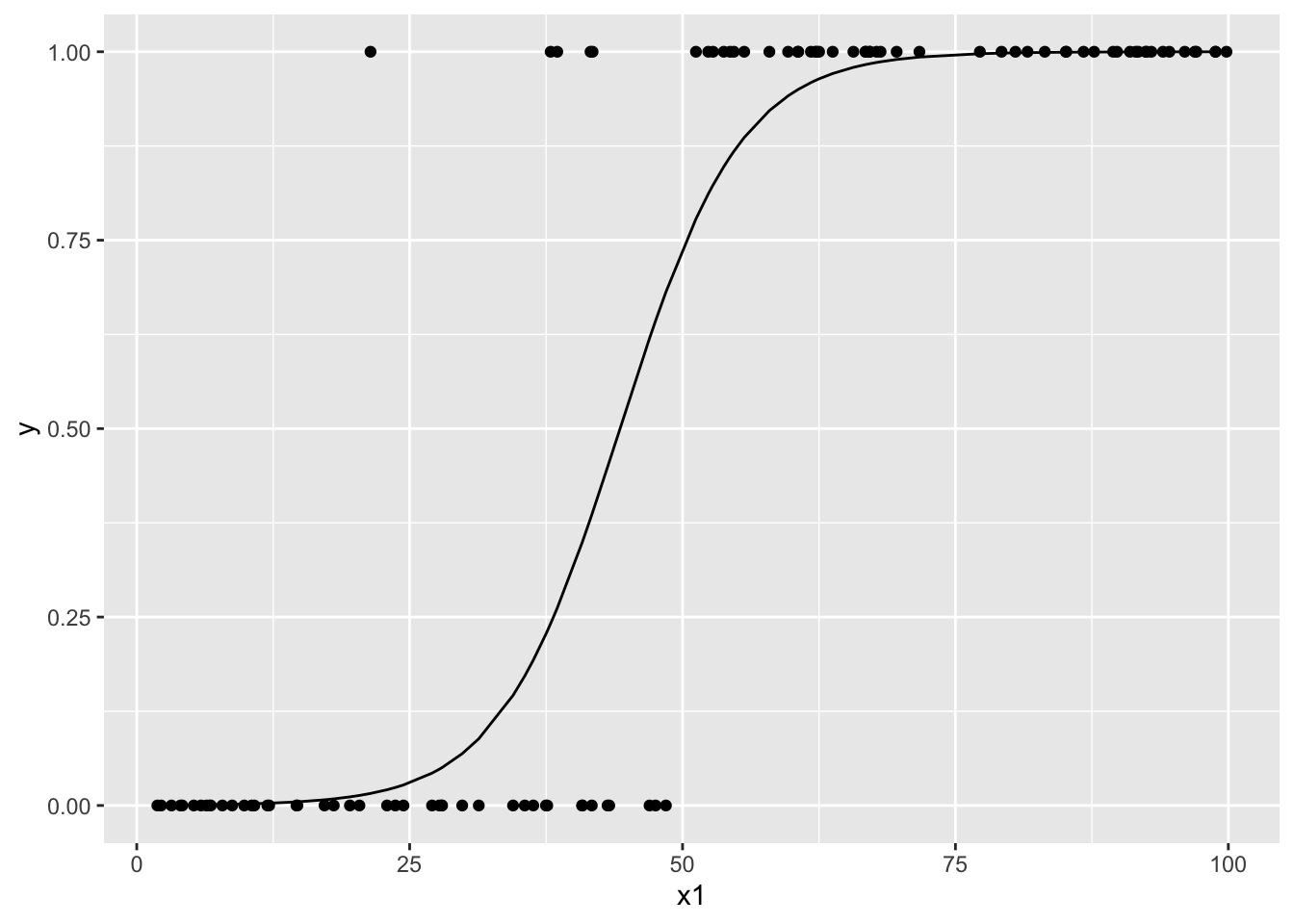

次にx2を追加投入したモデルを分析する．

glm(y ~ x1 + x2, data = data, 
    family = binomial(link = "logit")) %>%
    summary()
## 
## Call:
## glm(formula = y ~ x1 + x2, family = binomial(link = "logit"), 
##     data = data)
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -10.36748    2.74594  -3.776  0.00016 ***
## x1            0.20956    0.05332   3.930  8.5e-05 ***
## x2            1.93162    1.05997   1.822  0.06840 .  
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 137.628  on 99  degrees of freedom
## Residual deviance:  31.777  on 97  degrees of freedom
## AIC: 37.777
## 
## Number of Fisher Scoring iterations: 8

x2は5%水準で有意にならず，このデータだけでは効果があるとまではいえない．しかしAICは減少しているので追加投入モデルをよりよいモデルとして採用する．

12.6 本日の課題

Rスクリプトを実行した結果をWordにコンパイルしたファイルをLUNA提出