第6章 大数の法則と中心極限定理

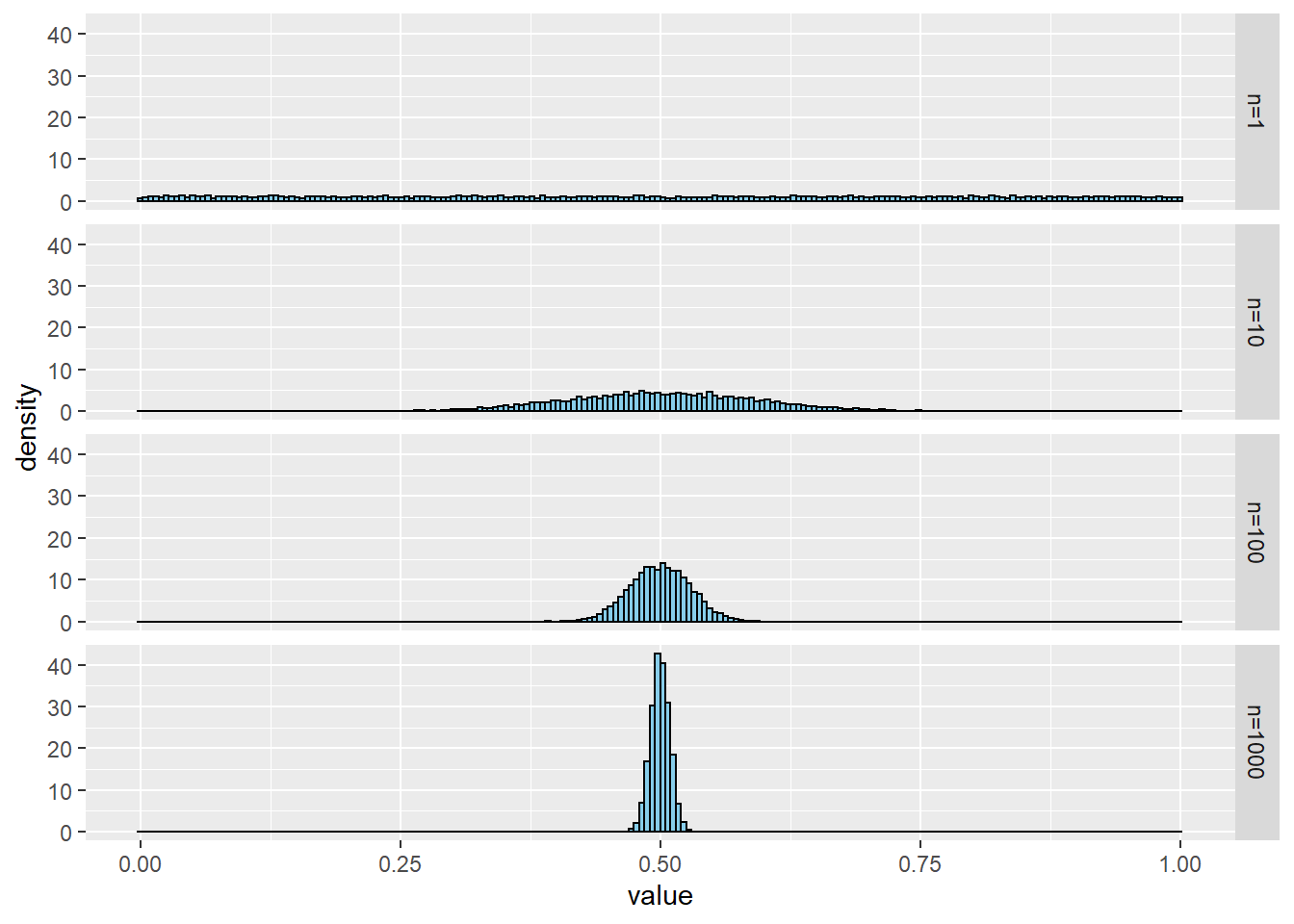
大数の法則と中心極限定理を実感するために，ランダムサンプリングデータの標本平均（相加平均）がどのような分布になるかを観察しよう．

6.1 一様分布からのランダムサンプリング

一様分布\(U(0,1)\)から，サンプルサイズ\(n=1,10,100,1000\)のサンプルをとって標本平均を計算する．これを，それぞれ10000回繰り返す．赤線は中心極限定理による標本分布近似の理論的予想である．

set.seed(8931)

repdata1<-replicate(10000,mean(runif(1,0,1)))
repdata2<-replicate(10000,mean(runif(10,0,1)))
repdata3<-replicate(10000,mean(runif(100,0,1)))
repdata4<-replicate(10000,mean(runif(1000,0,1)))

hist(repdata1, prob=TRUE, breaks = seq(0,1,0.005), 
     xlim=c(0,1), main = "n=1", xlab ="", col="skyblue")

hist(repdata2, prob=TRUE, breaks = seq(0,1,0.005),
     xlim=c(0,1), main = "n=10", xlab ="", col="skyblue")
curve(dnorm(x, mean=1/2, sd= sqrt(1/12)/sqrt(10)),
      type="l", col = "red", lwd=2, add=T)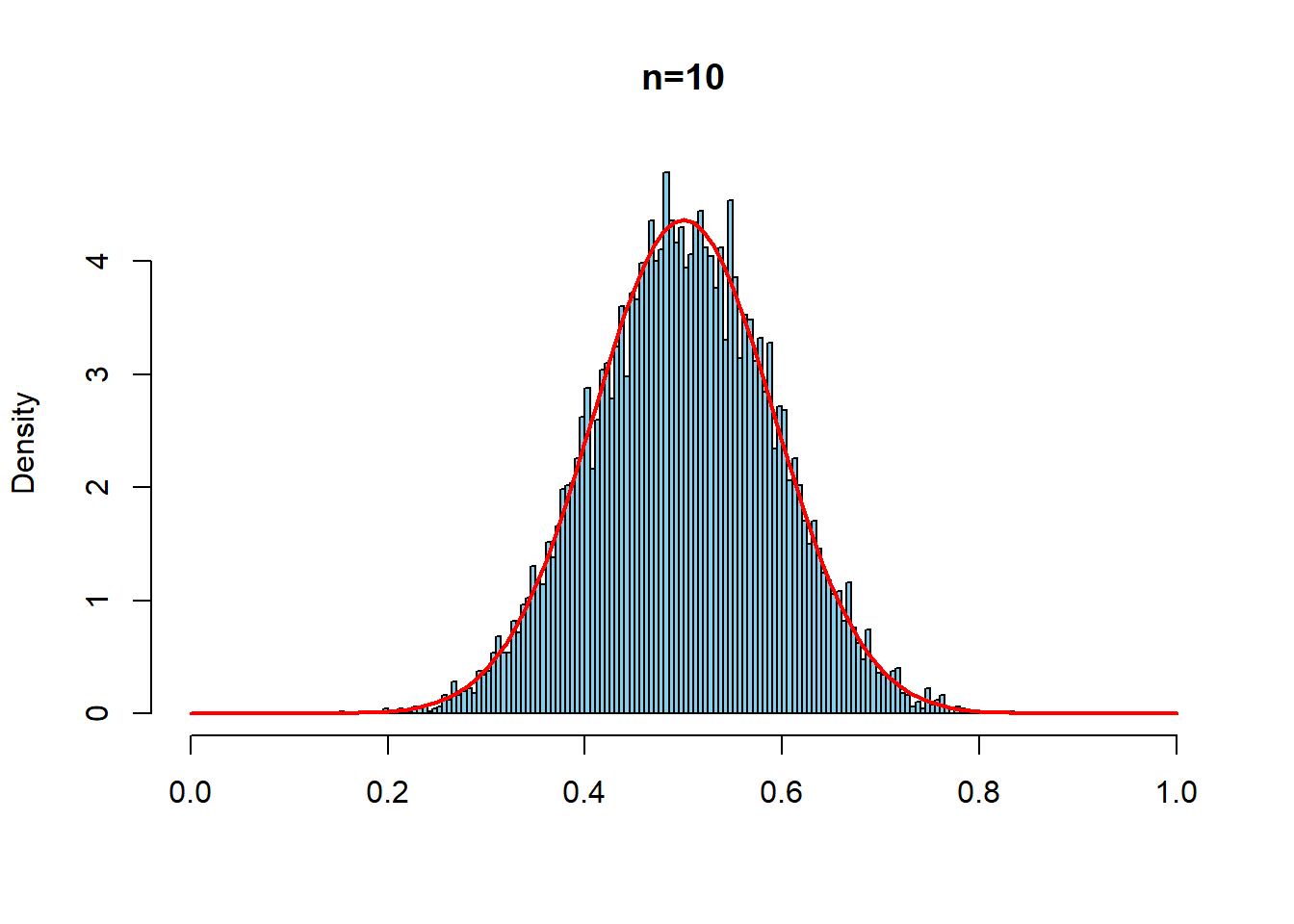

hist(repdata3, prob=TRUE, breaks = seq(0,1,0.005),
     xlim=c(0,1), main = "n=100", xlab ="", col="skyblue")
curve(dnorm(x, mean=1/2, sd= sqrt(1/12)/sqrt(100)),
      type="l", col = "red", lwd=2, add=T)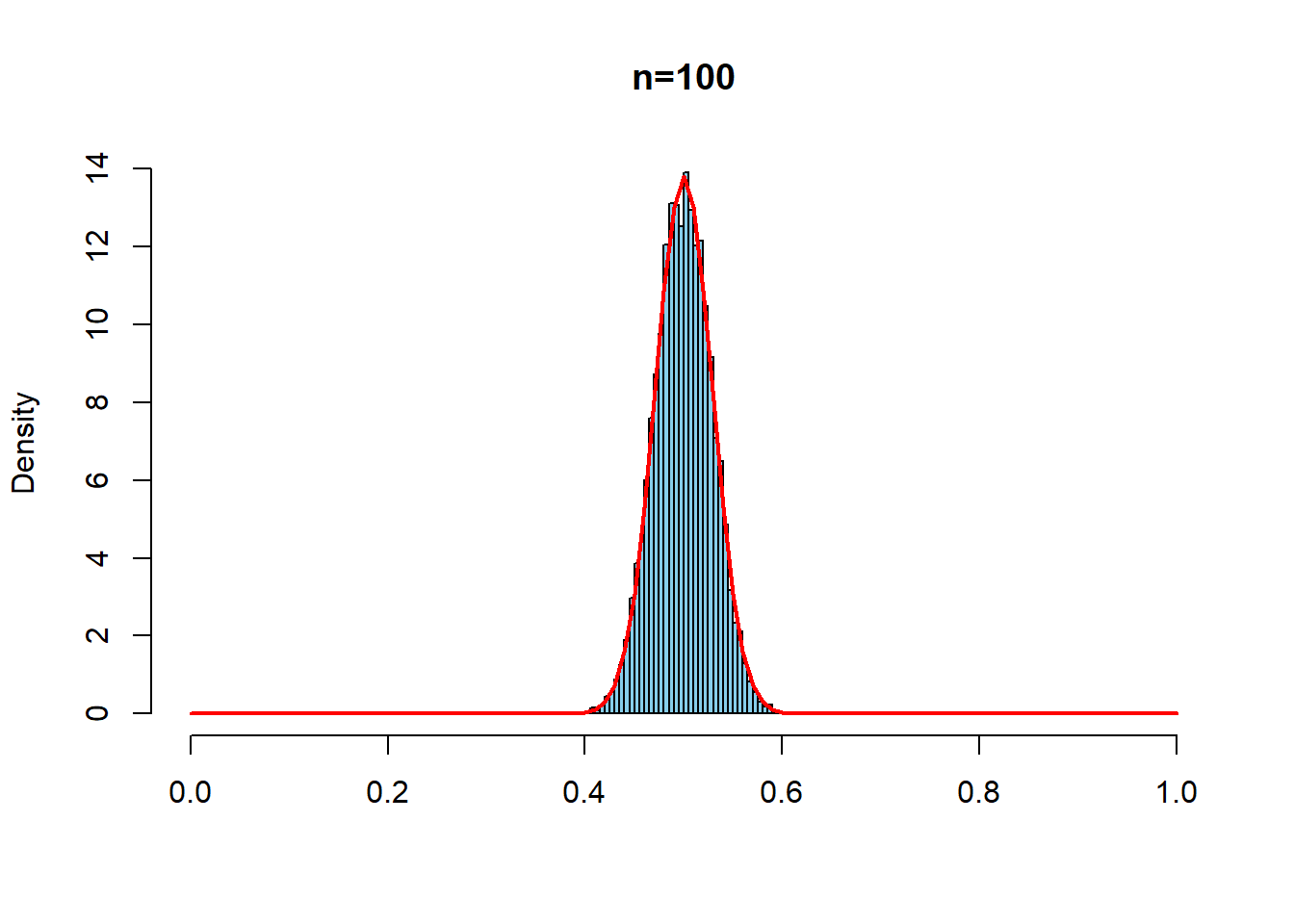

hist(repdata4, prob=TRUE, breaks = seq(0,1,0.005),
     xlim=c(0,1), main = "n=1000", xlab ="", col="skyblue")
curve(dnorm(x, mean=1/2, sd= sqrt(1/12)/sqrt(1000)),
      type="l", col = "red", add=T)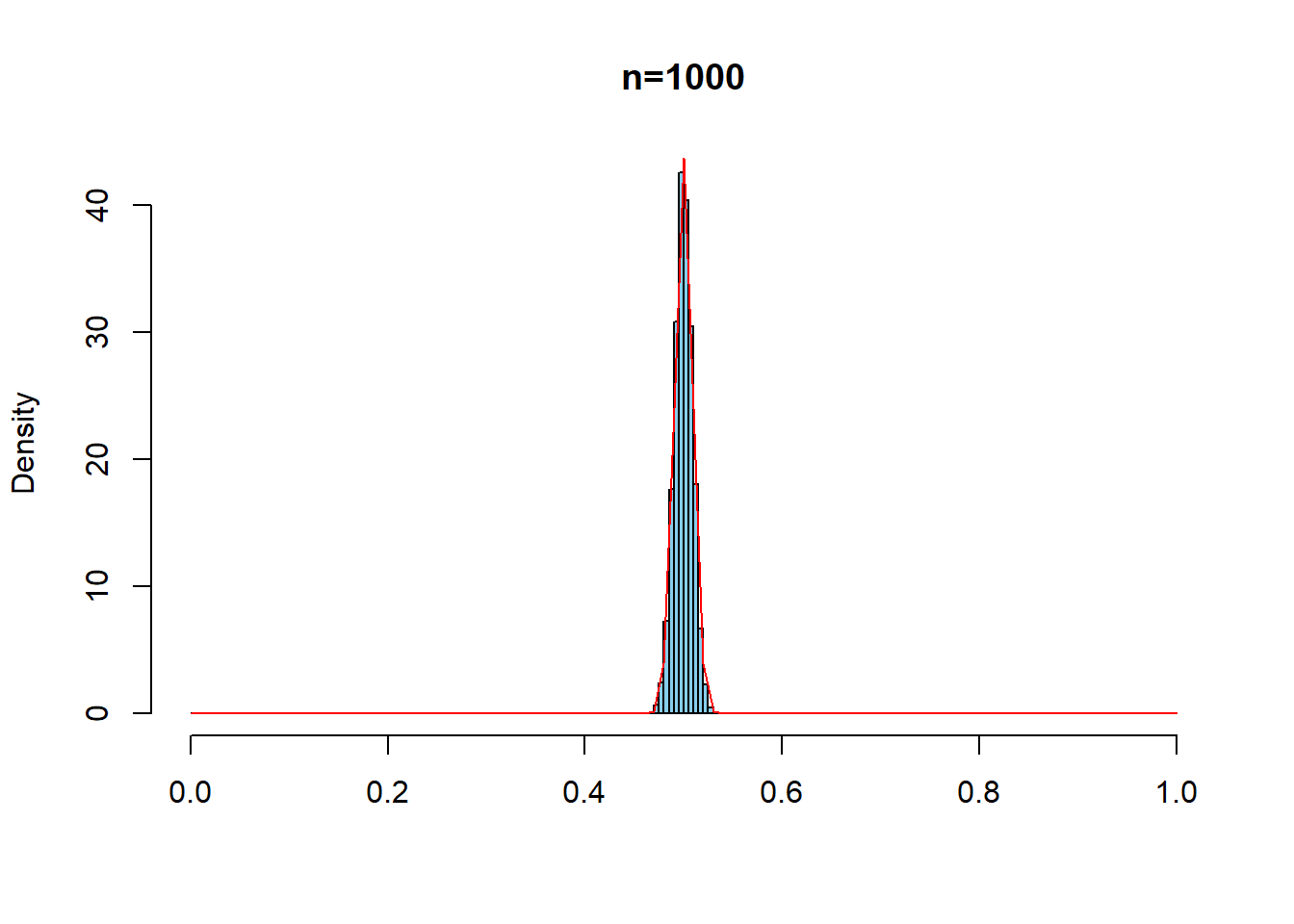

6.2 ベータ分布\(Beta(0.5,0.5)\)からのランダムサンプリング

同じことをよりゆがんだ分布としてベータ分布\(Beta(0.5,0.5)\)でもやってみる

repdata5<-replicate(10000,mean(rbeta(1,0.5,0.5)))
repdata6<-replicate(10000,mean(rbeta(10,0.5,0.5)))
repdata7<-replicate(10000,mean(rbeta(100,0.5,0.5)))
repdata8<-replicate(10000,mean(rbeta(1000,0.5,0.5)))
hist(repdata5, prob=TRUE, breaks = seq(0,1,0.005),
     xlim=c(0,1), main = "n=1", xlab ="", col="skyblue")

hist(repdata6, prob=TRUE, breaks = seq(0,1,0.005),
     xlim=c(0,1), main = "n=10", xlab ="", col="skyblue")
curve(dnorm(x, mean=1/2, sd= sqrt(1/8)/sqrt(10)),
      type="l", col = "red", lwd=2, add=T)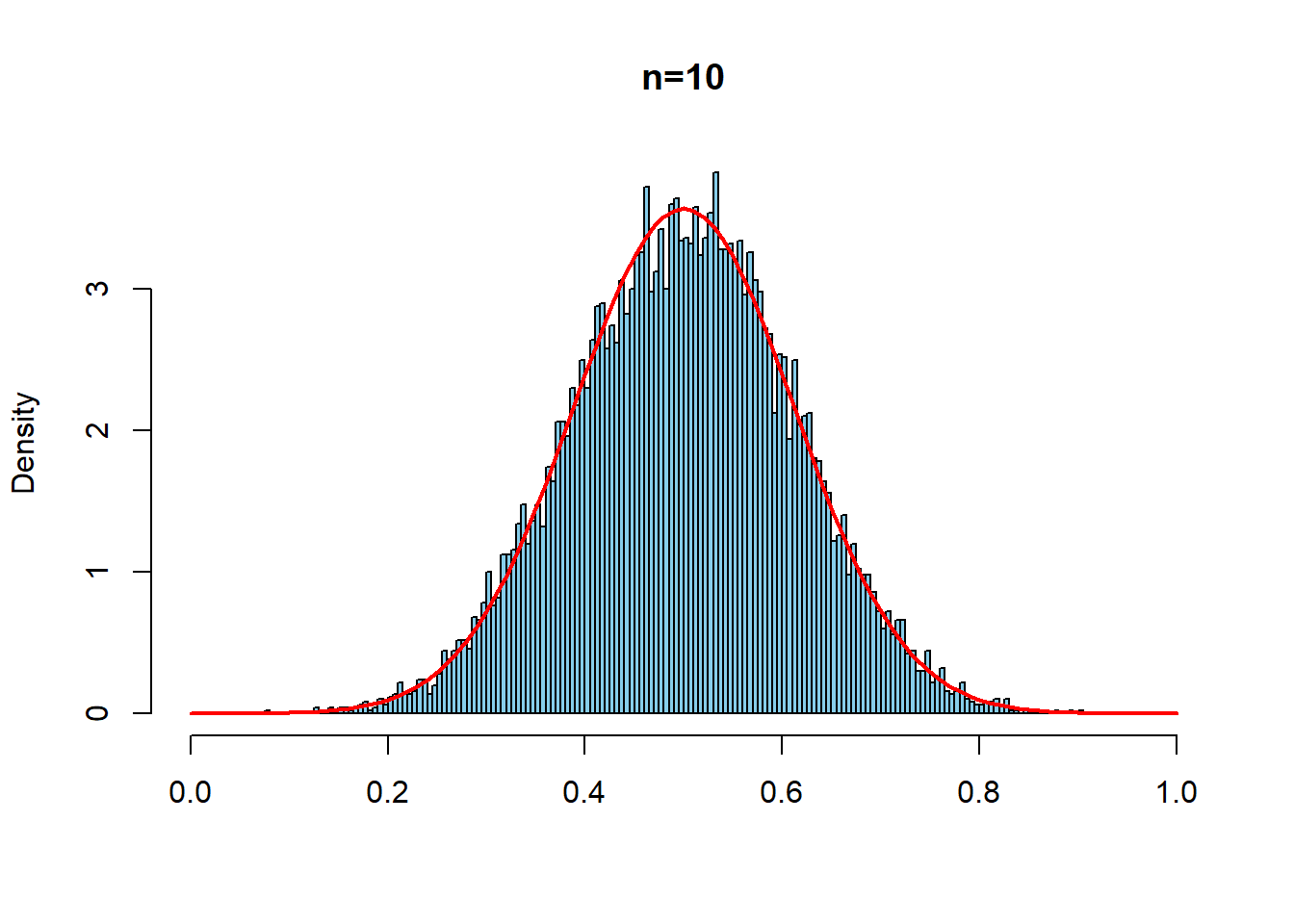

hist(repdata7, prob=TRUE, breaks = seq(0,1,0.005),
     xlim=c(0,1), main = "n=100", xlab ="", col="skyblue")
curve(dnorm(x, mean=1/2, sd= sqrt(1/8)/sqrt(100)),
      type="l", col = "red", lwd=2, add=T)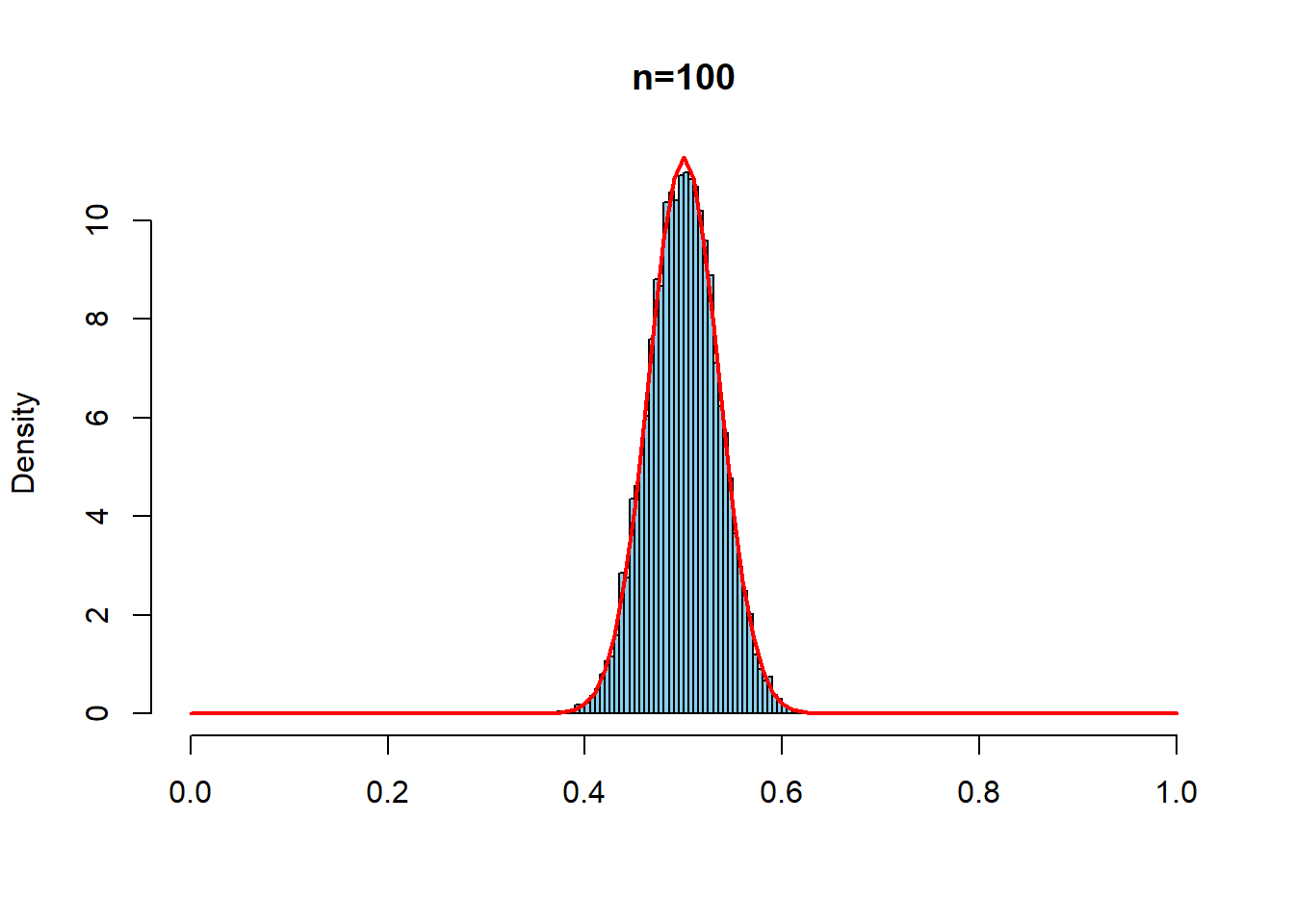

hist(repdata8, prob=TRUE, breaks = seq(0,1,0.005),
     xlim=c(0,1), main = "n=1000", xlab ="", col="skyblue")
curve(dnorm(x, mean=1/2, sd= sqrt(1/8)/sqrt(1000)),
      type="l", col = "red", lwd=2, add=T)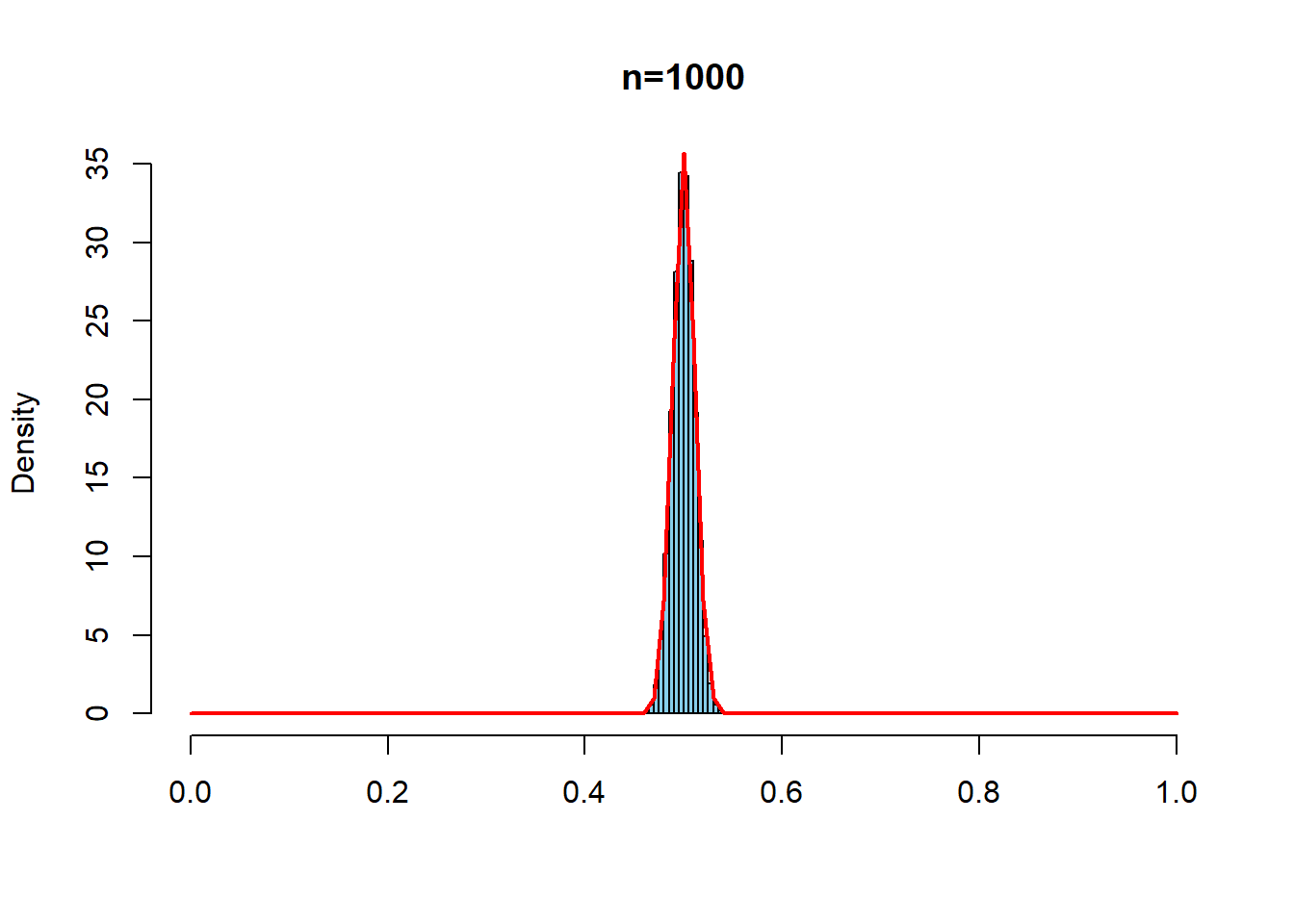

6.3 おまけggplotで書く

要tidyverse

library(tidyverse)
tibble("n=1"=repdata1,"n=10"=repdata2,
           "n=100"=repdata3,"n=1000"=repdata4) %>%
  pivot_longer(everything(), 
               names_to = "key",
               values_to = "value") %>%
  ggplot() +
  geom_histogram(aes(x = value, y =..density..),
                 bins=200,fill="skyblue", color= "black") +
  # geom_density(adjust = 4, colour='black', size=1.25) +
  facet_grid(key~.)