第3章 推測統計学の考え方
ここでは無作為抽出(ランダム.サンプリング)による統計的推測の威力を感じてみよう.まずは細かいことは置いておいて感覚を大づかみしてみよう.
3.1 データ
真の分布(母集団分布)が平均170,分散100の正規分布であるとしよう.ふつう,調査の段階ではこの真の分布はわかっていない.標本(サンプル)から真の分布を推測するのが統計的推測である.

3.2 ランダム・サンプリング
真の分布からサンプルサイズ10のサンプルをランダム・サンプリングする.
サンプルのヒストグラムは以下のようになる.
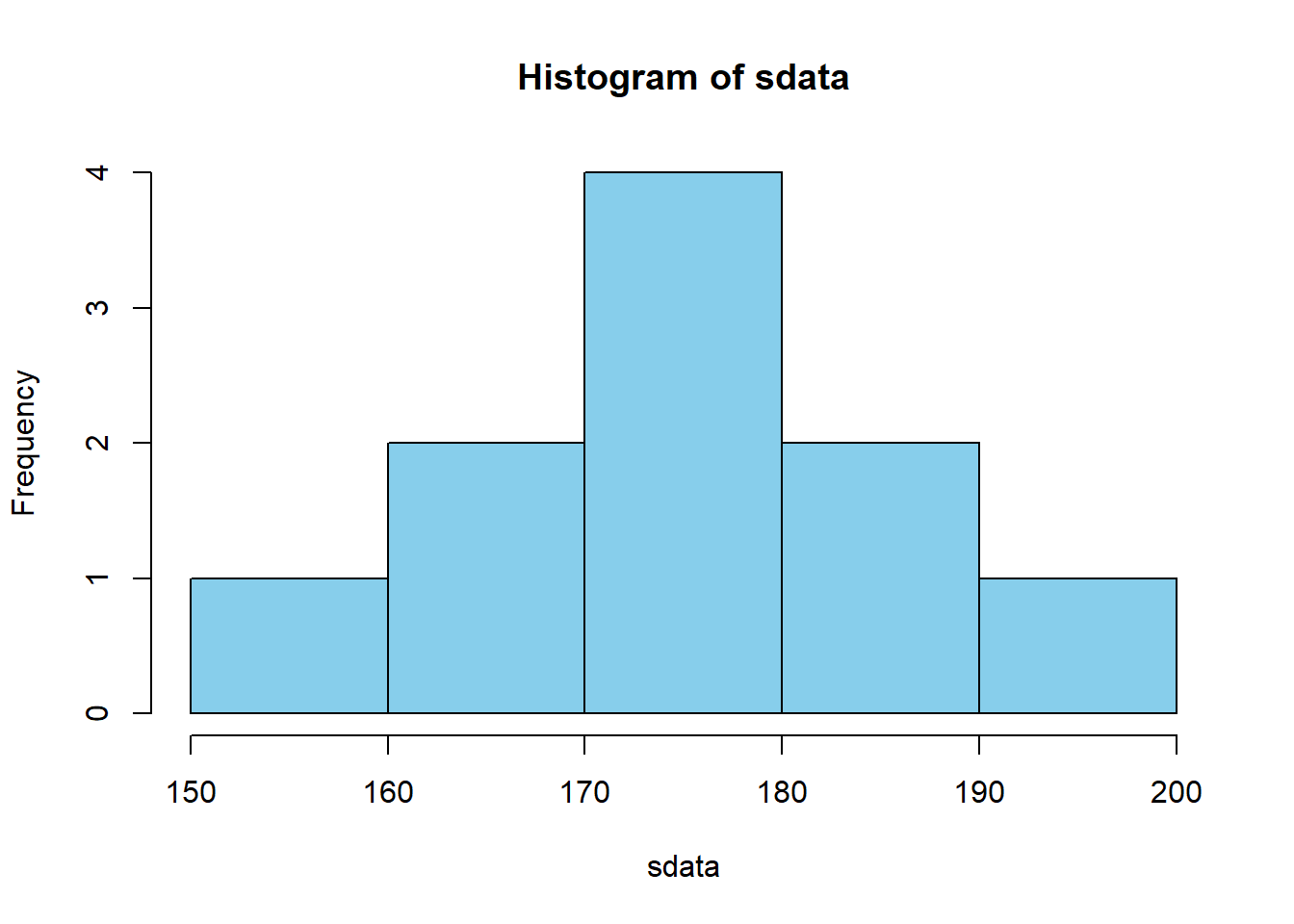
サンプルの平均と分散は以下のようになる.
## [1] 173.4489## [1] 126.29693.3 ランダム・サンプリングの繰り返し
真の分布からサンプルサイズ10のランダム・サンプルの平均をとる操作を10000回繰り返す.
そのデータのヒストグラムは以下のようになる.

そのデータの平均と分散は以下のようになる.
## [1] 169.9568## [1] 10.08717ランダム・サンプリング平均の繰り返しデータの平均は真の分布の平均をよく近似しているようだ(ここで,平均という言葉が3回出てくることに注意).
ところで,ランダム・サンプリング平均の繰り返しデータから,真の分布の分散を推定する場合は以下の公式を使う.
## [1] 100.87173.4 バイアスのあるサンプリングの場合
真の分布の中でも低めの値がサンプリングされやすいバイアスのあるサンプリングを考えてみよう.
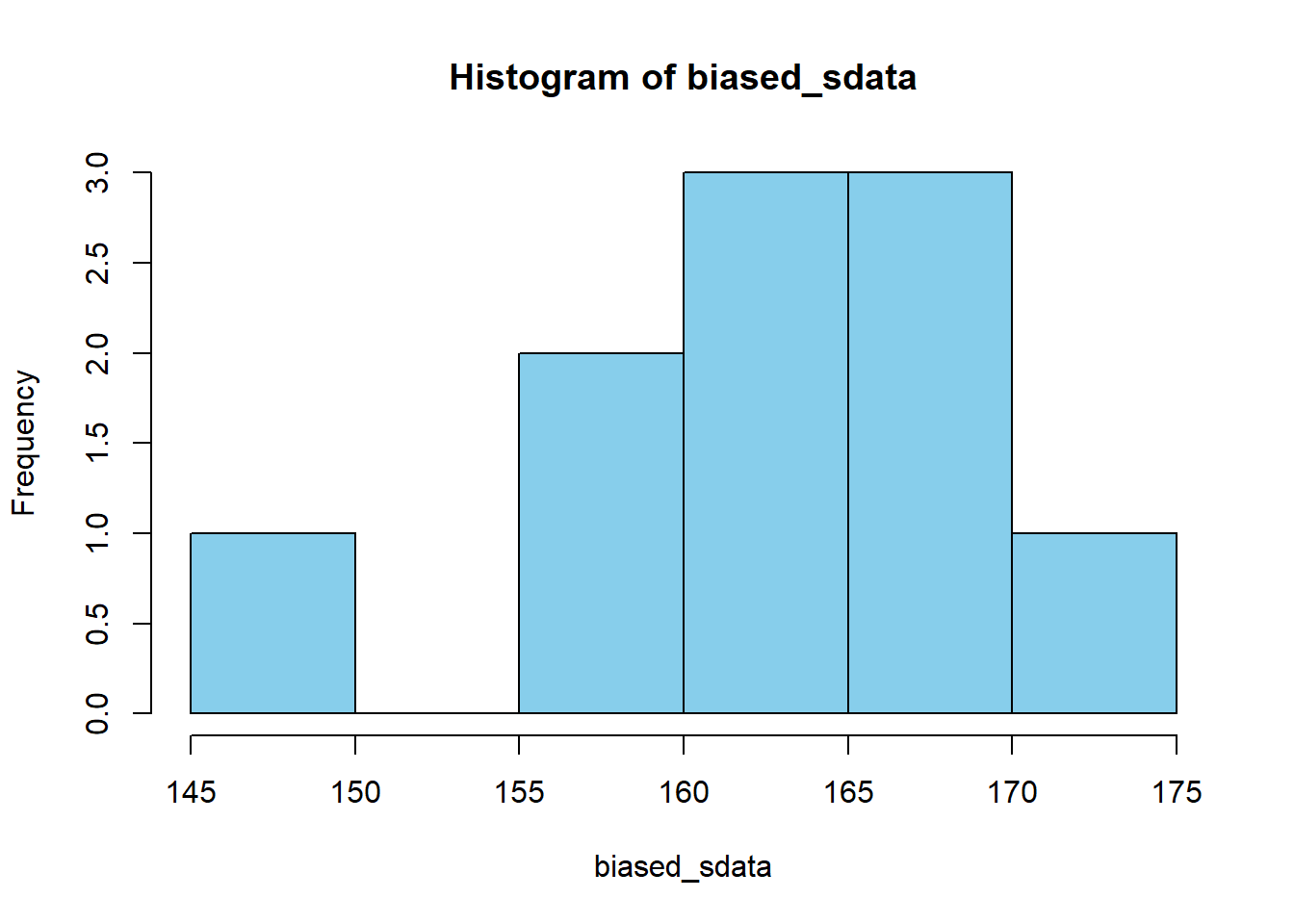
## [1] 162.483## [1] 42.6229バイアスのあるサンプリングをr回繰り返す.
そのデータのヒストグラムは以下のようになる.
hist(biased_rsdata, freq = FALSE, col = "skyblue")
lines(density(biased_rsdata), col = "blue", lwd = 2)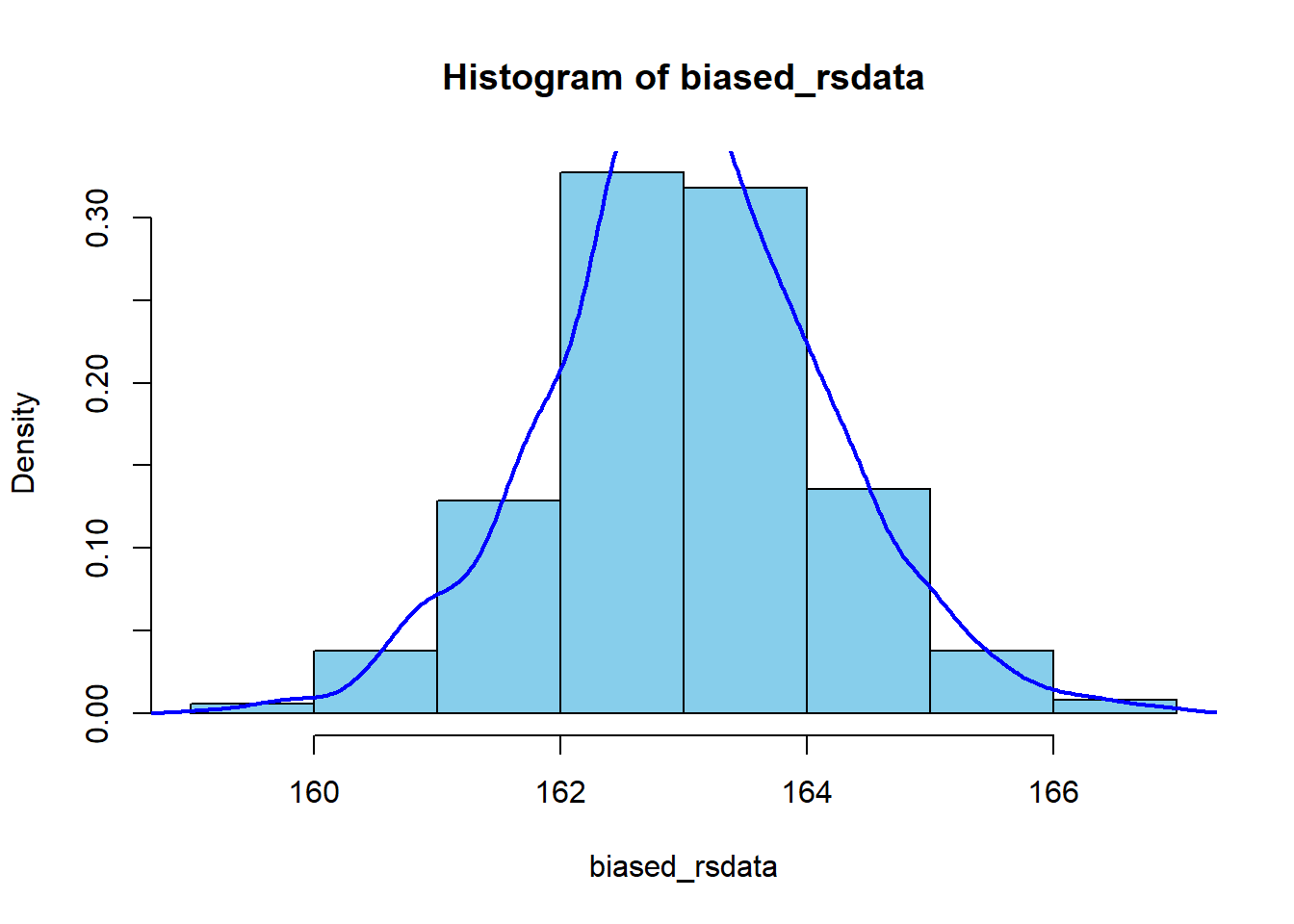
そのデータの平均と分散は以下のようになる.
## [1] 163.0292## [1] 1.274754真の分布の平均とずれがあるようだ.
最後にランダム・サンプリング(赤)とバイアスのあるサンプリング(青)の平均の分布を比較してみる.
hist(biased_rsdata, freq = FALSE,
col = "#0000ff40", border = "#0000ff",
breaks = 20,xlim = c(140, 200),main = "")
hist(rsdata, freq = FALSE,
col = "#ff00ff40", border = "#ff00ff",
breaks = 20,xlim = c(140, 200),add=TRUE)
lines(density(biased_rsdata), col = "blue", lwd = 2)
lines(density(rsdata), col = "red", lwd = 2)