第2章 記述統計学のおさらい

2.1 平均，分散，標準偏差

平均は以下のように定義される． \[\bar{x}=\frac{\sum_{i=1}^nx_i}{n}=\frac{x_1+x_2+\cdots +x_n}{n}\] Rで計算する場合は，定義通りsum(x)/length(x)とするか，組み込み関数を用いてmean(x)とする．講義ノート2.2.1の身長データの例．

x <- c(152.8, 150.1, 182.0, 163.2, 167.3, 
       160.2, 164.9, 161.4, 179.9, 172.2)
sum(x)/length(x)
## [1] 165.4
mean(x)
## [1] 165.4

平均の特性については平均を実感するも参照のこと．

分散の定義は以下の通りである． \[\hat{\sigma}^2=\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2}{n}\]

Rのデフォルトの分散関数var(x)は\(n-1\)で割る不偏分散である．講義ノートの定義の分散を計算させたい場合は，定義に基づく計算をそのまま行うか，var(x)に\((n-1)/n\)を掛ければよい．

mean((x-mean(x))^2)
## [1] 97.664
(length(x)-1)/length(x) * var(x)
## [1] 97.664

標準偏差は分散のルートを取ったものである． \[\hat{\sigma}=\sqrt{\hat{\sigma}^2}=\sqrt{\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2}\] Rのデフォルトの標準偏差関数はsd(x)であり，これは不偏分散のルートである．

sqrt(mean((x-mean(x))^2))
## [1] 9.88251
sqrt((length(x)-1)/length(x)) * sd(x)
## [1] 9.88251

分散の特性についてはばらつきを実感するも参照のこと．

2.2 標準得点

Rでscale(x)をもちいてベクトルを一括して標準得点に変換できる．ただし，標準偏差は\(n-1\)でわる定義を採用している．

\[z_i=\frac{x_i-\bar{x}}{\hat{\sigma}_x}\]

x_scaled <- scale(x)
as.vector(x_scaled)
##  [1] -1.2095520 -1.4687417  1.5935368 -0.2111916  0.1823928 -0.4991802
##  [7] -0.0479981 -0.3839848  1.3919448  0.6527741
mean(x_scaled)
## [1] -5.412337e-16
sd(x_scaled)
## [1] 1

標準化については標準化を実感するも参照のこと．

2.3 共分散と相関係数

2変数の関係を散布図で確認する．

x <- c(152.8,150.1,182,163.2,167.3,160.2,164.9,161.4,179.9,172.2)
y <- c(56.3,52.1,85.6,66.8,74.2,58.1,61.9,55.1,70.5,64.1)
plot(x,y)

また，tidyverseに含まれるggplot2で散布図を書くと以下のようになる．パッケージを用いる場合は，先にlibrary(tidyverse)を実行してパッケージを呼び出しておく．

library(tidyverse)
## -- Attaching packages --------------- tidyverse 1.3.0 --
## √ ggplot2 3.3.0     √ purrr   0.3.4
## √ tibble  3.0.1     √ dplyr   0.8.5
## √ tidyr   1.0.3     √ stringr 1.4.0
## √ readr   1.3.1     √ forcats 0.5.0
## -- Conflicts ------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()
tibble(x = c(152.8,150.1,182,163.2,167.3,160.2,164.9,161.4,179.9,172.2),
       y = c(56.3,52.1,85.6,66.8,74.2,58.1,61.9,55.1,70.5,64.1)) %>% 
  ggplot() +
  geom_point(aes(x = x, y = y))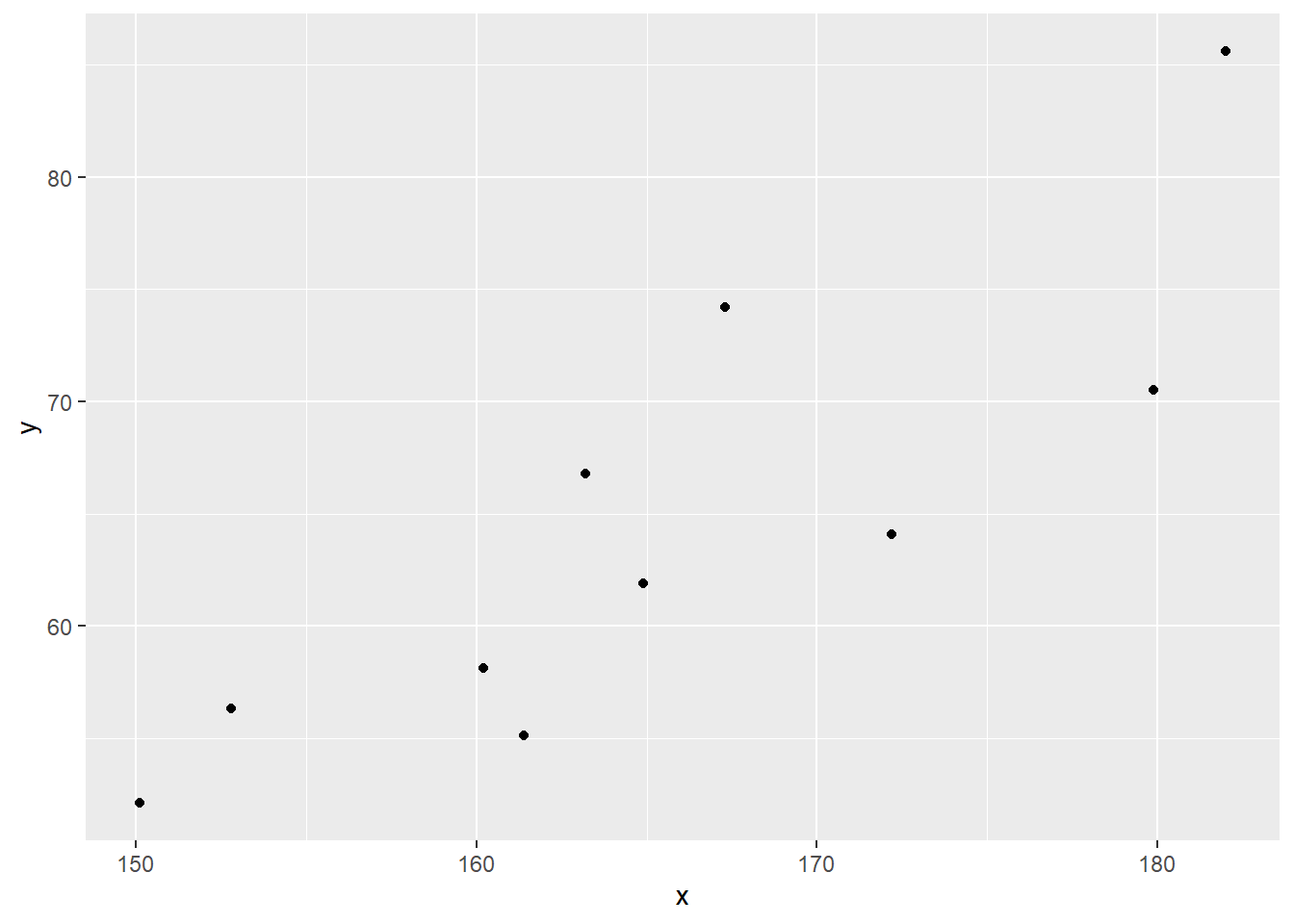

次に，共分散を計算する．

\[\begin{align*} c_{xy}&=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) \\ &=\frac{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n} \nonumber \end{align*}\]

Rで共分散はcov(x, y)であり，\(n-1\)でわる定義を採用している．

mean((x-mean(x))*(y-mean(y)))
## [1] 81.313
cov(x,y)*(length(x)-1)/length(x)
## [1] 81.313

相関係数は，標準化した2変数の共分散であり， \[r_{xy}=\frac{c_{xy}}{\hat{\sigma}_x\hat{\sigma}_y}\] で計算できる．Rでは相関係数関数cor(x,y)が用意されている．公式通りcov(x,y)/(sd(x)*sd(y))としてもよい（基準化されている値なので\(n\)で割るか\(n-1\)で割るかは関係ない）．

cov(x,y)/(sd(x)*sd(y))
## [1] 0.8496357
cor(x,y)
## [1] 0.8496357