第7章 標本と標本分布

ここでは，標本平均の標本分布をシミュレーションによって確かめてみる．

set.seed(8931)

7.1 一様分布からの\(z\)値の標本分布

一様分布\(U(0,1)\)から，サンプルサイズ\(n=5,10,30,100\)のサンプルをとる．

母平均\(\mu=1/2\)，母分散\(\sigma^2=1/12\)はわかっているので，標本平均\(\bar{X}\)の\(Z\)値を \[Z=\frac{\bar{X}-\mu}{\sqrt{\sigma^2/n}}=\frac{\bar{X}-1/2}{\sqrt{1/(12n)}}\] によって算出する．理論的には，\(n\)が十分大きいとき，\(Z\)の分布は標準正規分布に近似するはずである．

以下，\(n\)を変えて検証する．赤は標準正規分布である．

n1<-5
repdata1<-replicate(10000,runif(n1))
z1<-apply(repdata1,2, function(x) {
  (mean(x)-1/2)/sqrt((1/12)/n1)
  })
hist(z1, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(z1))),ceiling(max(abs(z1))),0.2),
     col="skyblue", main = paste("n =",n1))
# lines(density(z1,adjust=2),lwd=2)
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)

n2<-10
repdata2<-replicate(10000,runif(n2))
z2<-apply(repdata2,2, function(x) {
  (mean(x)-1/2)/sqrt((1/12)/n2)
})
hist(z2, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(z2))),ceiling(max(abs(z2))),0.2),
     col="skyblue", main = paste("n =", n2))
# lines(density(z2,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)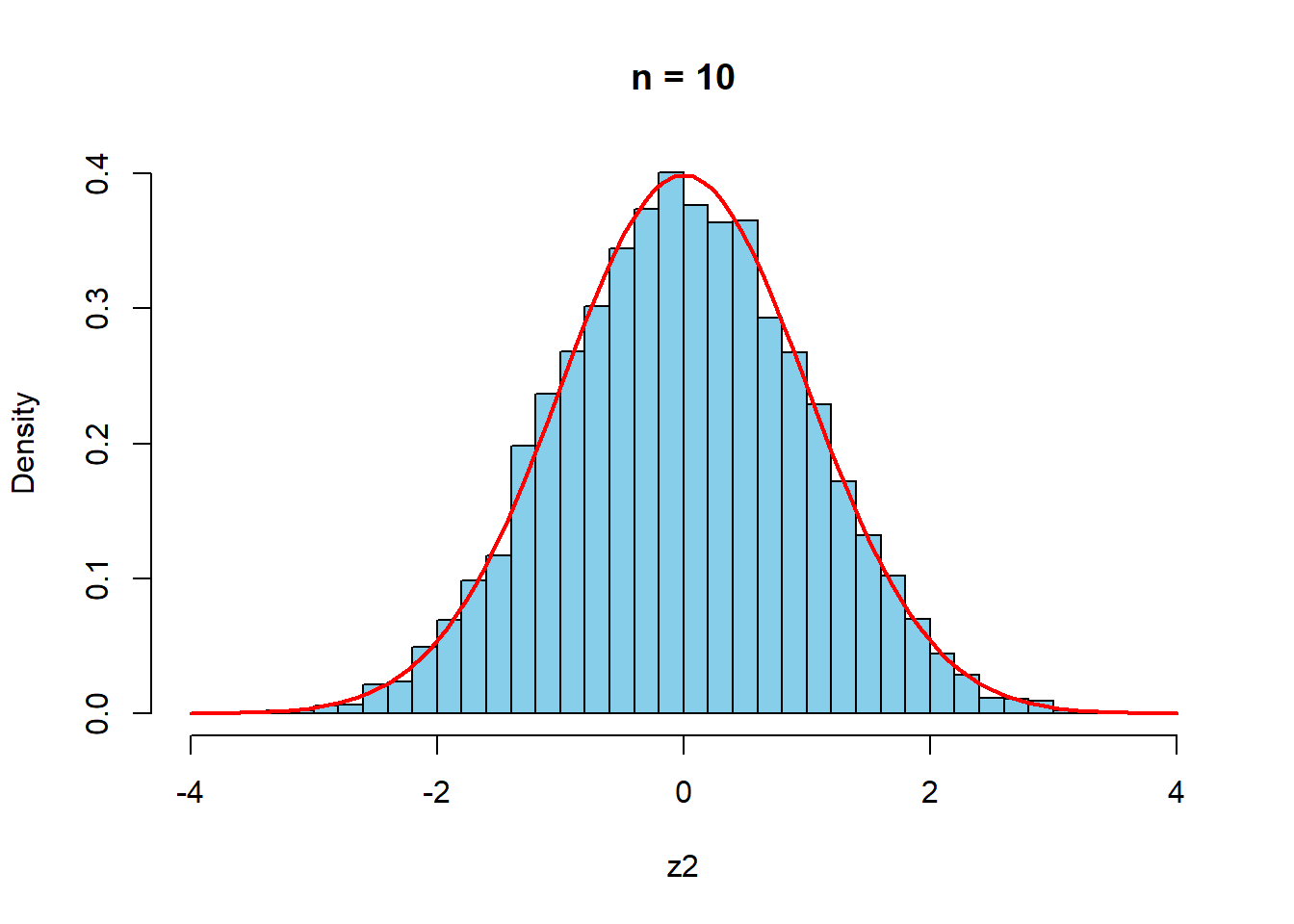

n3<-30
repdata3<-replicate(10000,runif(n3))
z3<-apply(repdata3,2, function(x) {
  (mean(x)-1/2)/sqrt((1/12)/n3)
})
hist(z3, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(z3))),ceiling(max(abs(z3))),0.2),
     col="skyblue", main = paste("n =", n3))
# lines(density(z3,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)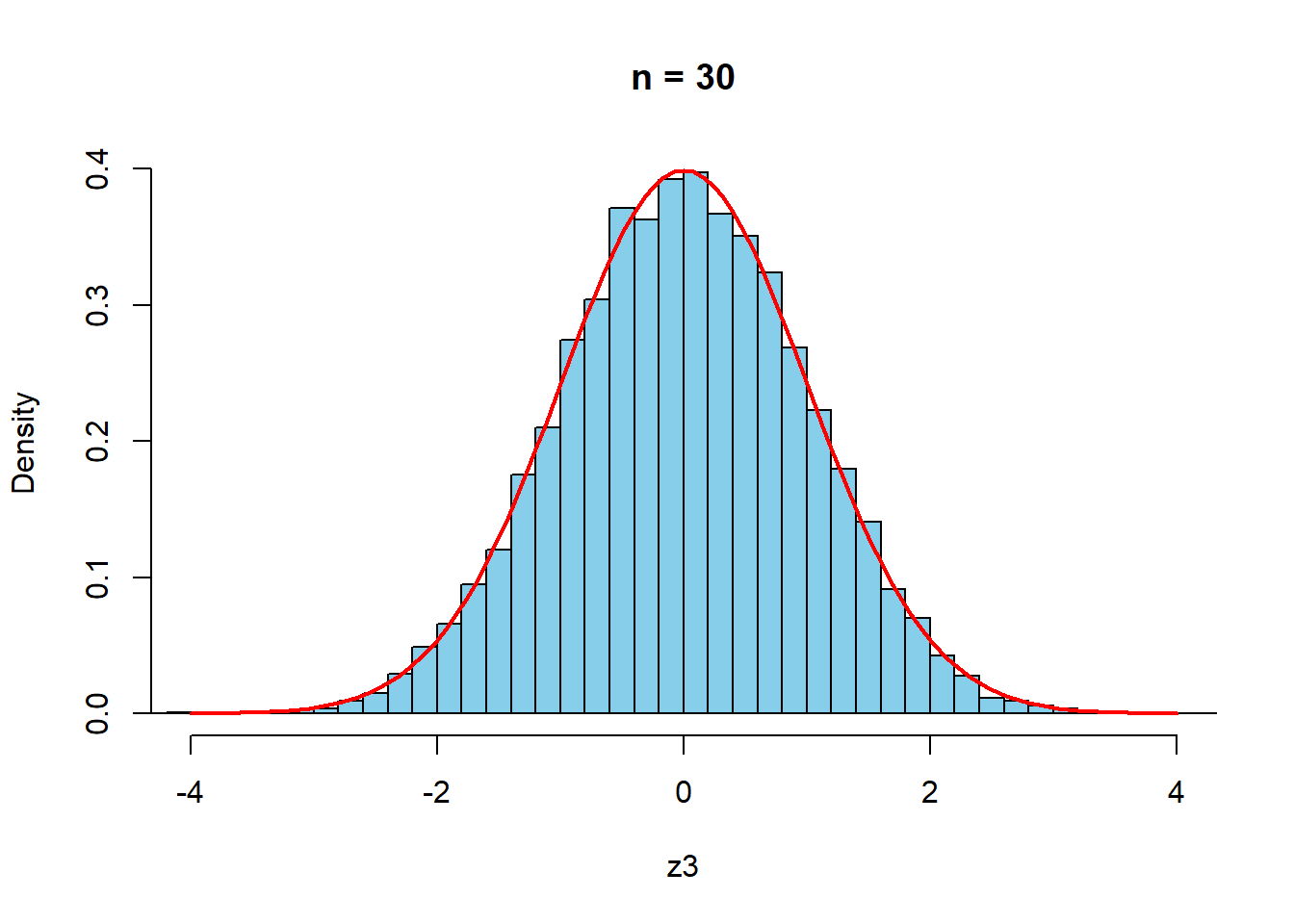

n4<-100
repdata4<-replicate(10000,runif(n4))
z4<-apply(repdata4,2, function(x) {
  (mean(x)-1/2)/sqrt((1/12)/n4)
})
hist(z4, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(z4))),ceiling(max(abs(z4))),0.2),
     col="skyblue", main = paste("n =", n3))
# lines(density(z4,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)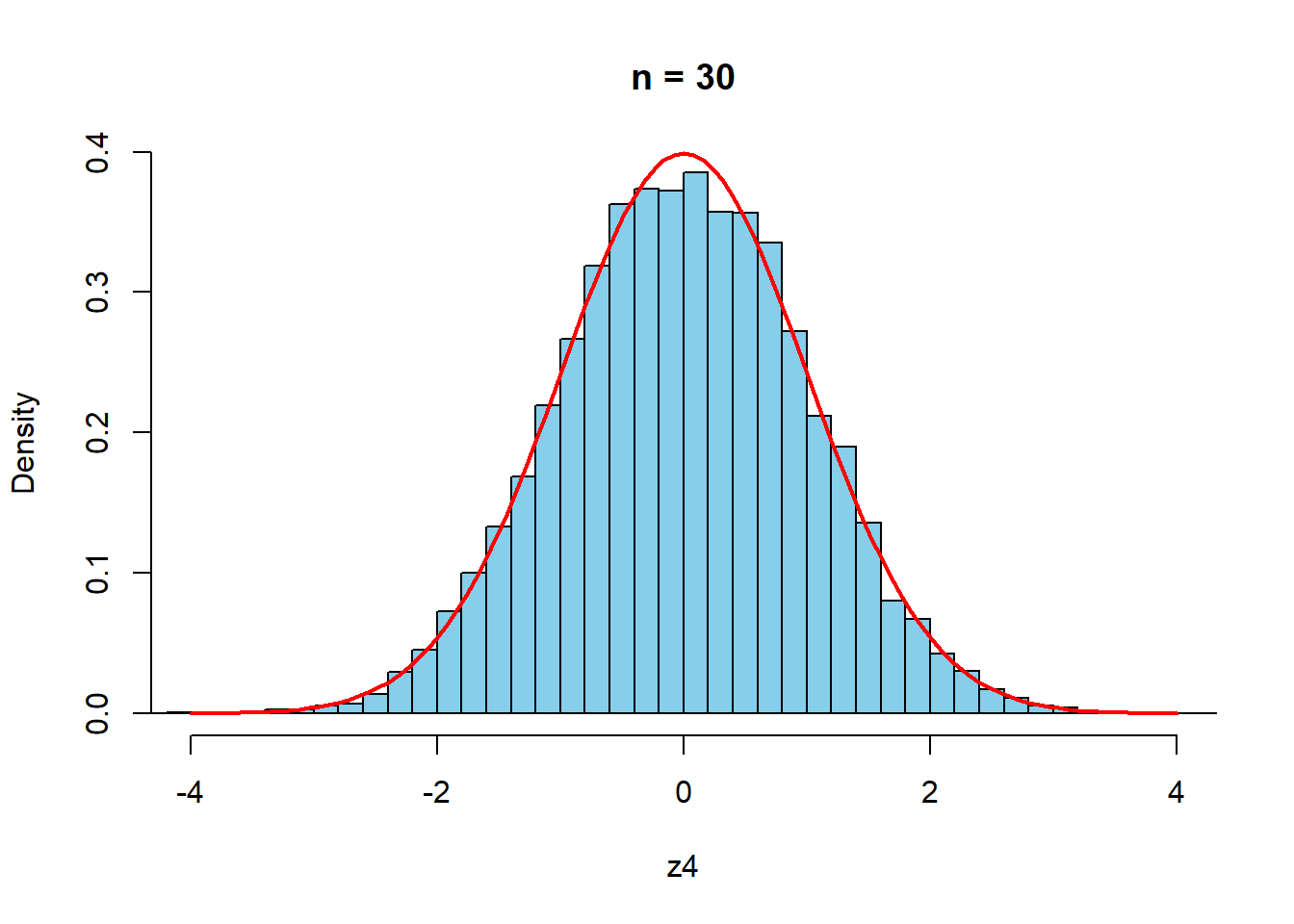

\(n=30\)程度で，十分近似しているといえそうである．

7.2 正規分布からの\(t\)値の標本分布

つぎに，母平均\(\mu=1\)，母分散\(\sigma^2=1\)の正規分布\(N(1,1)\)からのサンプルで\(t\)値を算出する．ここでは，母平均は既知だが，母分散は未知と考え，不偏標本分散\(S^2\)で置き換える． \[t=\frac{\bar{X}-\mu}{\sqrt{S^2/n}}=\frac{\bar{X}-1}{\sqrt{S^2/n}}\] 理論的には，\(t\)値は自由度\(n-1\)の\(t\)分布に近似し，\(n\)が十分に大きければ\(t\)値は標準正規分布に近似すると考えられる．

以下，\(n\)を変えて検証する．赤は標準正規分布，青は自由度\(n-1\)の\(t\)分布である．

n5<-5
repdata5<-replicate(10000,rnorm(n5,1,1))
t5<-apply(repdata5,2, function(x) {
  (mean(x)-1)*sqrt(n5)/sd(x)
})
hist(t5, prob=TRUE,xlim=c(-6,6),
     breaks=seq(-ceiling(max(abs(t5))),ceiling(max(abs(t5))),0.2),
     col="skyblue", main = paste("n =", n5))
# lines(density(t5,adjust=2))
curve(dnorm(x,0,1),-6,6,col="red",lwd=2,add=TRUE)
curve(dt(x,n5-1),-6,6,col="blue",lwd=2,add=TRUE)

n6<-10
repdata6<-replicate(10000,rnorm(n6,1,1))
t6<-apply(repdata6,2, function(x) {
  (mean(x)-1)*sqrt(n6)/sd(x)
})
hist(t6, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(t6))),ceiling(max(abs(t6))),0.2),
     col="skyblue", main = paste("n =", n6))
# lines(density(t6,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)
curve(dt(x,n6-1),-4,4,col="blue",lwd=2,add=TRUE)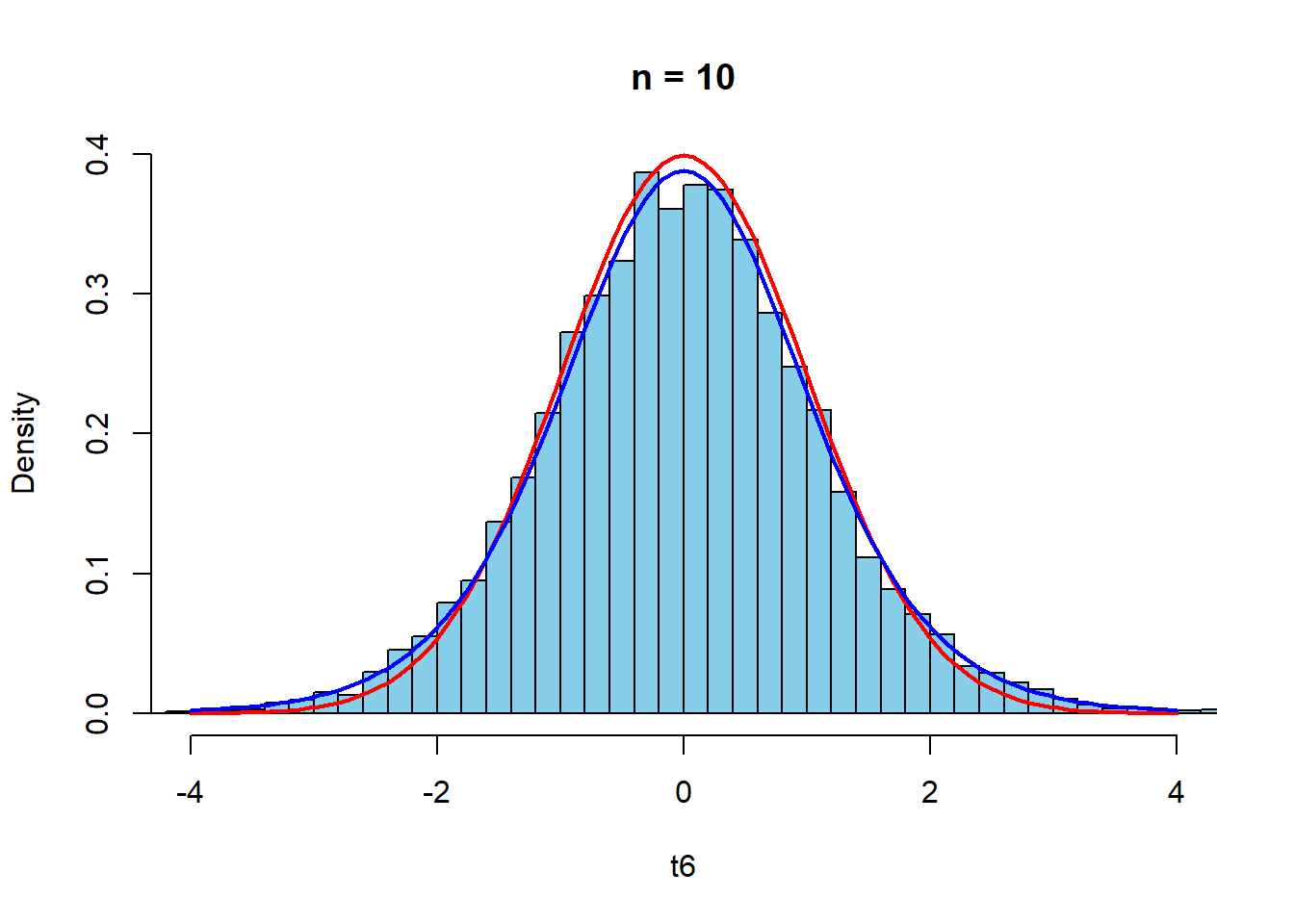

n7<-30
repdata7<-replicate(10000,rnorm(n7,1,1))
t7<-apply(repdata7,2, function(x) {
  (mean(x)-1)*sqrt(n7)/sd(x)
})
hist(t7, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(t7))),ceiling(max(abs(t7))),0.2),
     col="skyblue", main = paste("n =", n7))
# lines(density(t7,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)
curve(dt(x,n7-1),-4,4,col="blue",lwd=2,add=TRUE)

n8<-100
repdata8<-replicate(10000,rnorm(n8,1,1))
t8<-apply(repdata8,2, function(x) {
  (mean(x)-1)*sqrt(n8)/sd(x)
})
hist(t8, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(t8))),ceiling(max(abs(t8))),0.2),
     col="skyblue", main = paste("n =", n8))
# lines(density(t8,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)
curve(dt(x,n8-1),-4,4,col="blue",lwd=2,add=TRUE)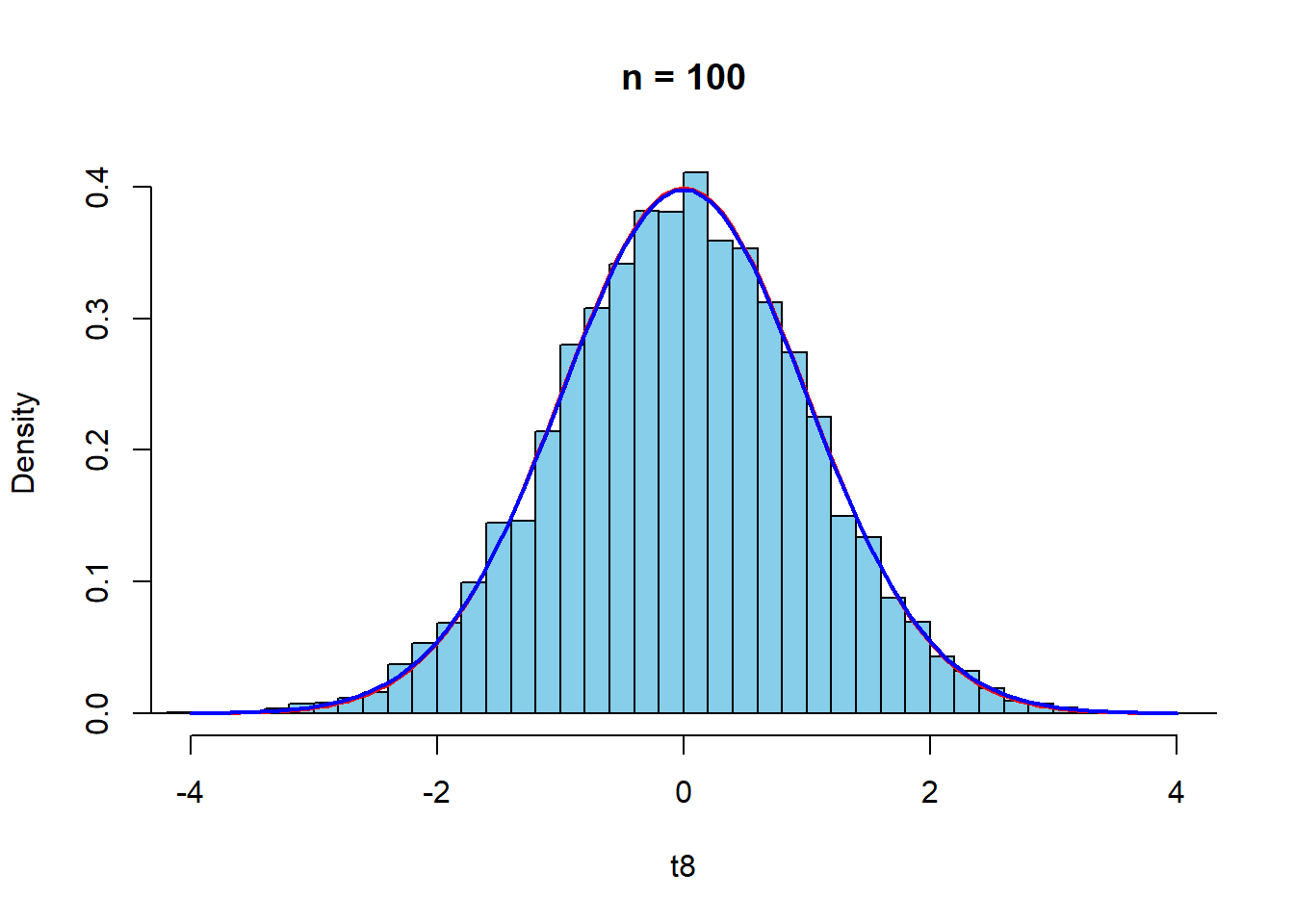

まず，\(n=5,10\)のときは，標準正規分布よりも\(t\)分布$のほうが近似がよい． \(n=30\)程度で，標準正規分布と\(t\)分布はほとんど等しくなり，経験密度関数との近似も高まる．

7.3 一様分布からの\(t\)値の標本分布

さいごに，一様分布\(U(0,1)\)からの\(t\)値の分布も確認する． \[t=\frac{\bar{X}-\mu}{\sqrt{S^2/n}}=\frac{\bar{X}-1/2}{\sqrt{S^2/n}}\] 理論的には，\(n\)が十分大きくなると，\(t\)値は標準正規分布に近似するはずである．

以下，\(n\)を変えて検証する．赤は標準正規分布，青は自由度\(n-1\)の\(t\)分布である．

t1<-apply(repdata1,2, function(x) {
  (mean(x)-1/2)*sqrt(n1)/sd(x)
})
hist(t1, prob=TRUE,xlim=c(-6,6),
     breaks=seq(-ceiling(max(abs(t1))),ceiling(max(abs(t1))),0.2),
     col="skyblue", main = paste("n =", n1))
# lines(density(t1,adjust=2))
curve(dnorm(x,0,1),-6,6,col="red",lwd=2,add=TRUE)
curve(dt(x,n1-1),-6,6,col="blue",lwd=2,add=TRUE)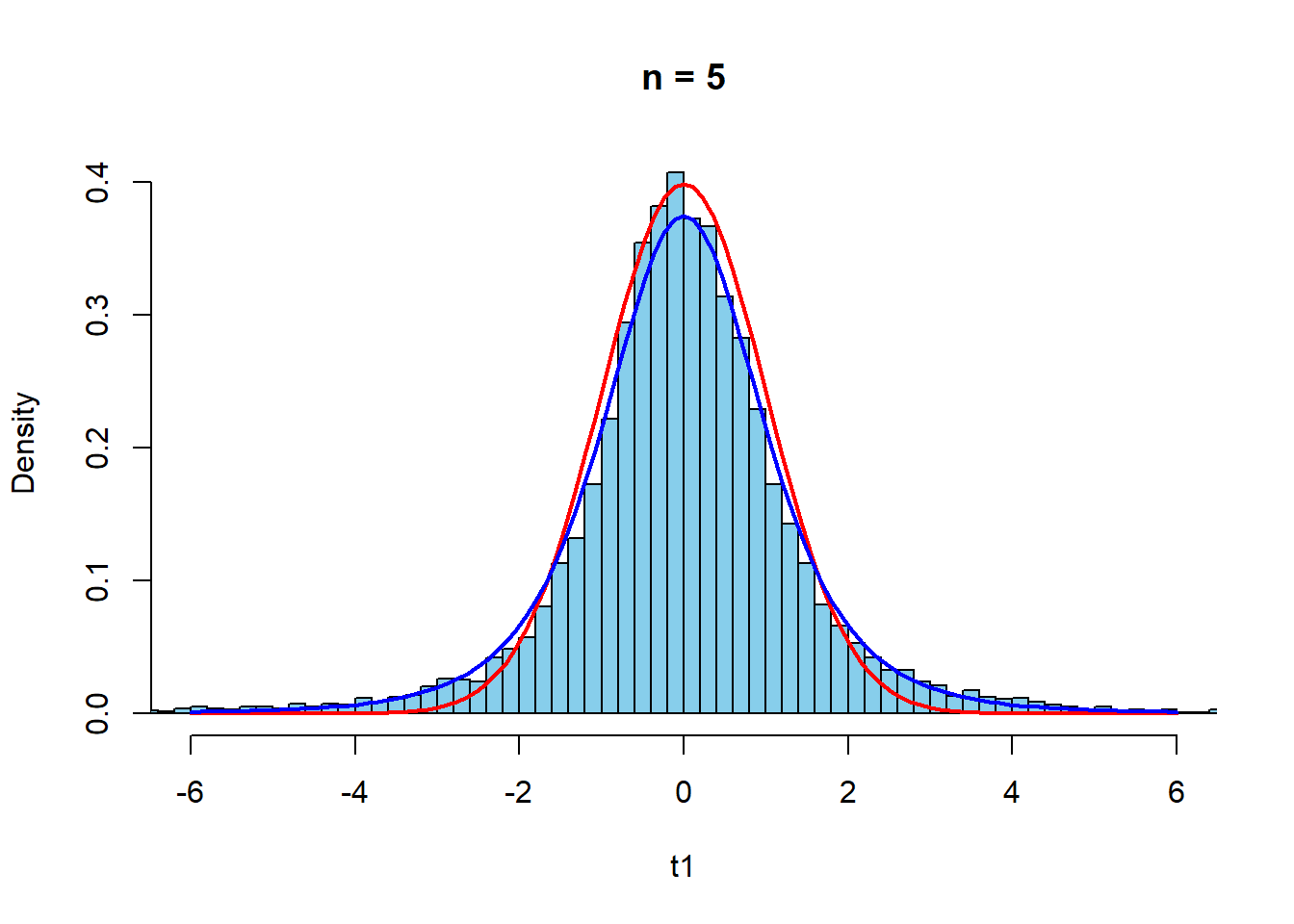

t2<-apply(repdata2,2, function(x) {
  (mean(x)-1/2)*sqrt(n2)/sd(x)
})
hist(t2, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(t2))),ceiling(max(abs(t2))),0.2),
     col="skyblue", main = paste("n =", n2))
# lines(density(t2,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)
curve(dt(x,n2-1),-4,4,col="blue",lwd=2,add=TRUE)

t3<-apply(repdata3,2, function(x) {
  (mean(x)-1/2)*sqrt(n3)/sd(x)
})
hist(t3, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(t3))),ceiling(max(abs(t3))),0.2),
     col="skyblue", main = paste("n =", n3))
# lines(density(t3,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)
curve(dt(x,n3-1),-4,4,col="blue",lwd=2,add=TRUE)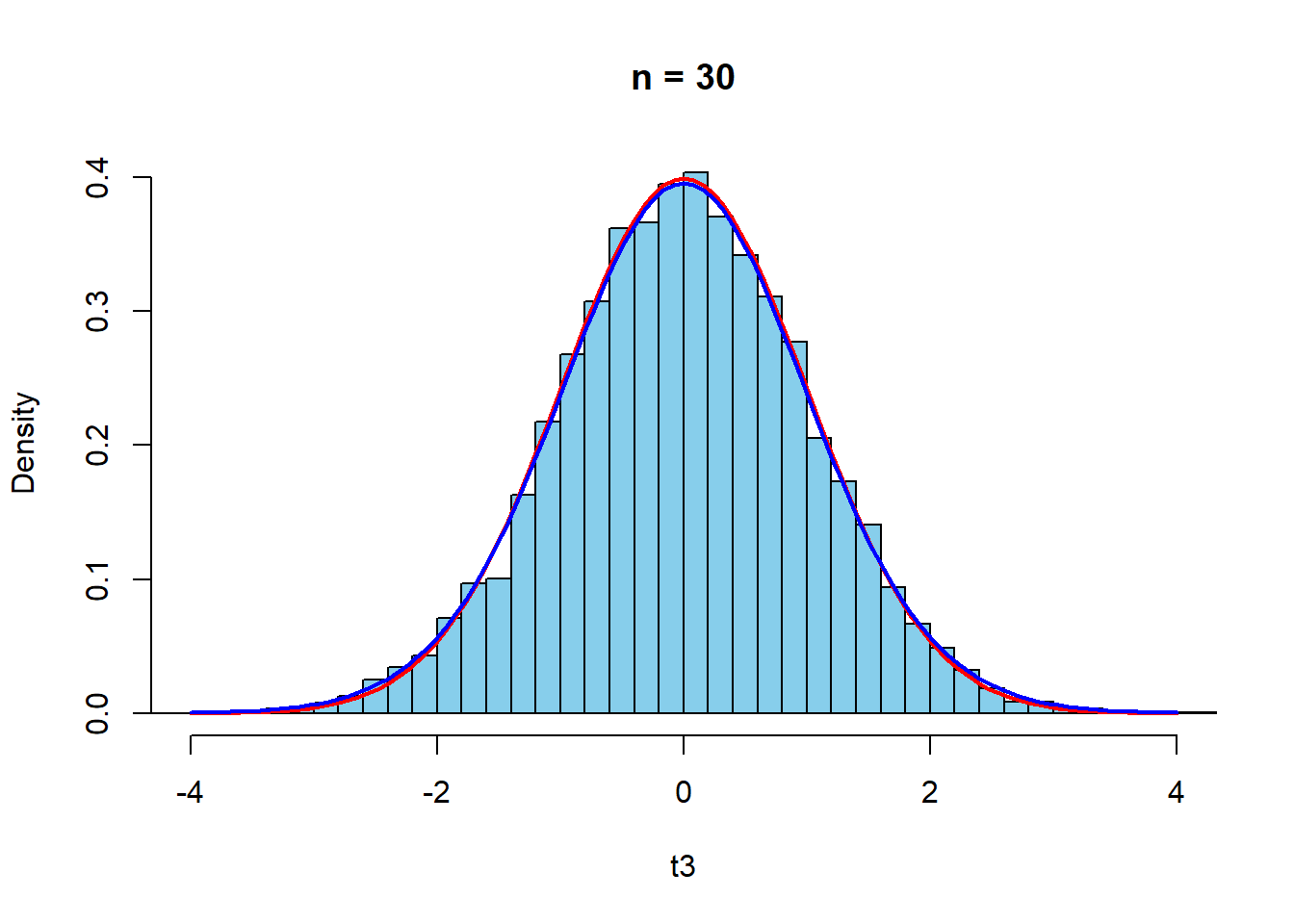

# n4<-100
# repdata4<-replicate(10000,runif(n4))
t4<-apply(repdata4,2, function(x) {
  (mean(x)-1/2)*sqrt(n4)/sd(x)
})
hist(t4, prob=TRUE,xlim=c(-4,4),
     breaks=seq(-ceiling(max(abs(t4))),ceiling(max(abs(t4))),0.2),
     col="skyblue", main = paste("n =", n4))
# lines(density(t4,adjust=2))
curve(dnorm(x,0,1),-4,4,col="red",lwd=2,add=TRUE)
curve(dt(x,n4-1),-4,4,col="blue",lwd=2,add=TRUE)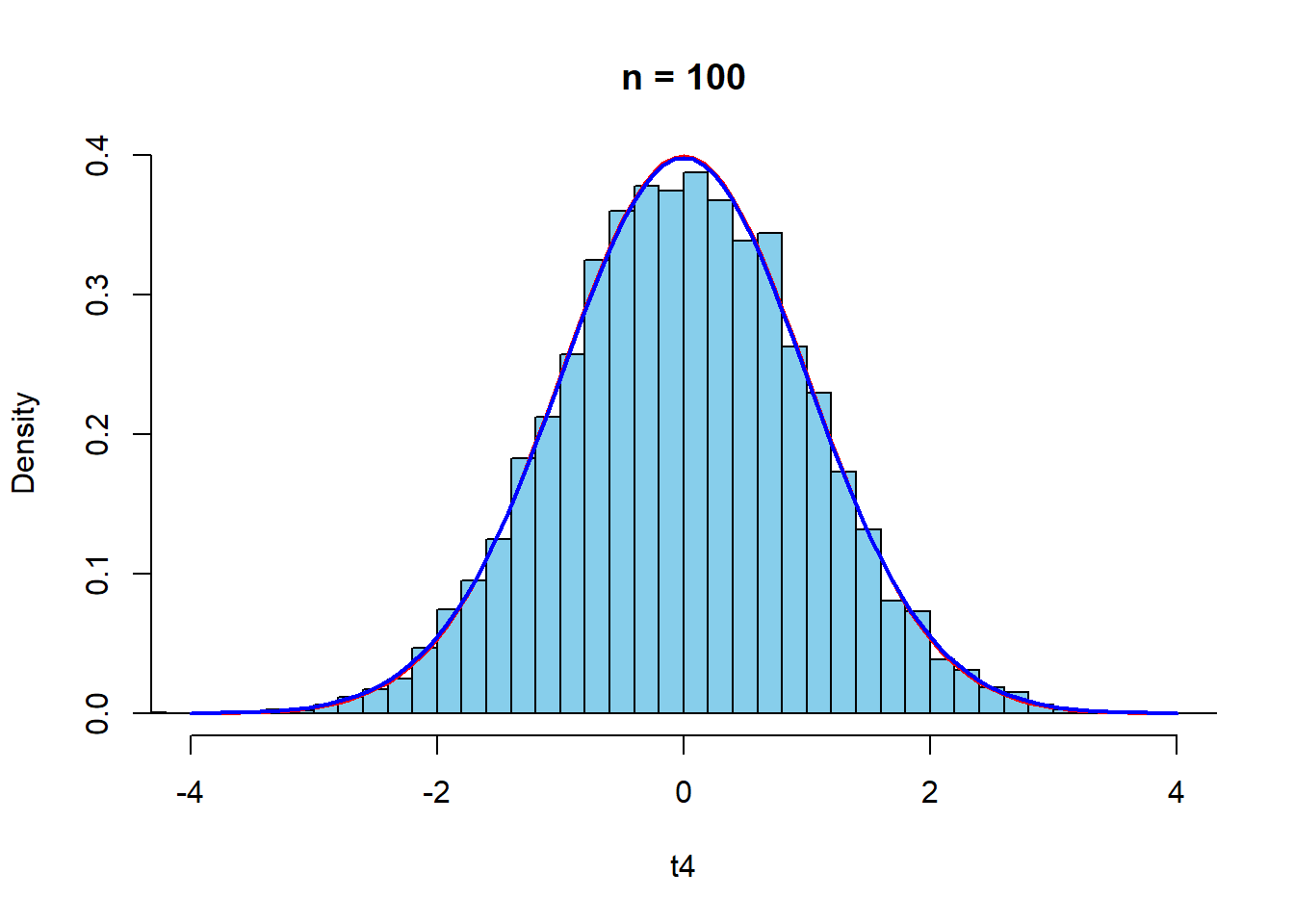

正規分布からの\(t\)値の標本分布と同様の傾向である．