第5章 確率変数と確率分布

ここでは，二項分布のグラフをRで描く方法を説明する．

5.1 二項分布

Rには，主要な確率分布の確率関数（連続の場合は確率密度関数）がすでに用意されている．二項分布はdbinom(x, size, prob)である．xが成功回数のベクトル，sizeは試行回数\(n\)，probは成功確率\(p\)を指定する．

5.2 二項分布のグラフ

基本的には，\(n\)(x<-0:5の5の値)と\(p\)の値を変えて一つずつグラフを描けばよい．

p<-0.5
x<-0:5
prob<-dbinom(x, length(x)-1, p)
names(prob)<-x
barplot(prob,col="skyblue")

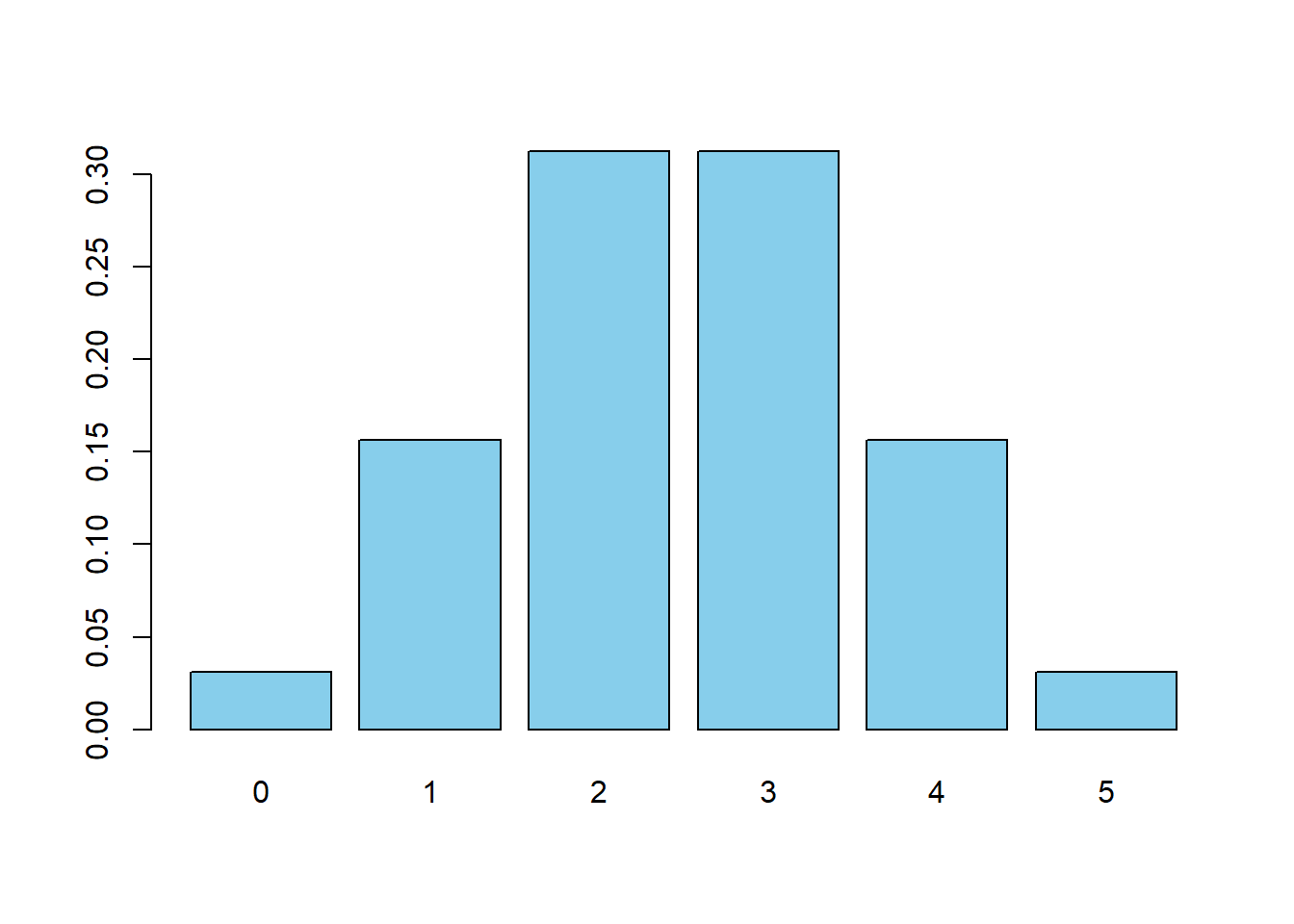
\(p\)を変えたグラフをまとめて描く．

\(n = 5\)

pvec<-c(0.1,0.5,0.7)
x<-0:5
probs<-sapply(pvec, function(p) dbinom(x, length(x)-1, p))
colnames(probs)<-c("p=0.1","p=0.5","p=0.7")
rownames(probs)<-x
barplot(t(probs),beside=TRUE, legend = TRUE,
        col=c("blue", "red", "green"))

\(n = 10\)

pvec<-c(0.1,0.5,0.7)
x<-0:10
probs<-sapply(pvec, function(p) dbinom(x, length(x)-1, p))
colnames(probs)<-c("p=0.1","p=0.5","p=0.7")
rownames(probs)<-x
barplot(t(probs),beside=TRUE, legend = TRUE,
        col=c("blue", "red", "green"))

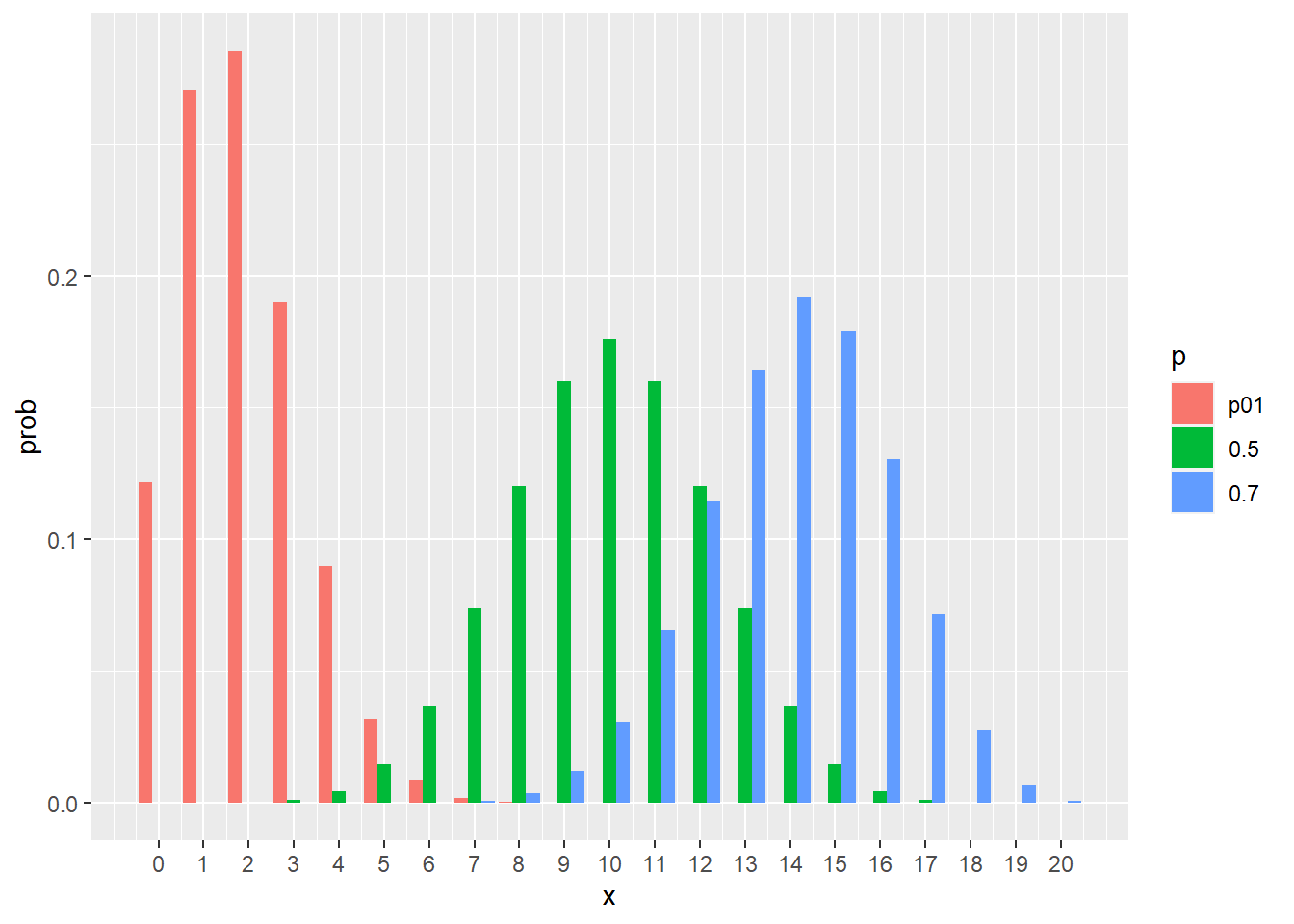
5.3 ggplot2で描く

モダンなグラフ描写をする場合は，ggplot2パッケージを用いるといいだろう．いくつかのパッケージをバンドルしたtidyverseパッケージを呼び出して使おう．

library(tidyverse)
x <- 0:20
tibble(
  x = x,
  p01 = dbinom(x, length(x) - 1, 0.1),
  p05 = dbinom(x, length(x) - 1, 0.5),
  p07 = dbinom(x, length(x) - 1, 0.7)
) %>% 
  gather(key = p, value = prob, p01, p05, p07) %>% 
  ggplot(.,aes(x=x,y=prob,fill=p)) +
  geom_bar(stat = "identity", position = "dodge") +
  scale_x_continuous(breaks = x) +
  scale_fill_hue(name = "p",
                  labels = c(p03 = "0.1",
                             p05 = "0.5",
                             p07 = "0.7"))